练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率是$\frac{\sqrt{2}}{2}$，F1、F2是椭圆的左、右焦点，点A为椭圆的右顶点，点B为椭圆的上顶点，且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）若直线l过右焦点F2且交椭圆E于P、Q两点，点M是直线x=2上的任意一点，直线MP、MF2、MQ的斜率分别为k1、k2、k3，问是否存在常数λ，使得k1+k3=λk2成立？若存在，求出λ的值；若不存在，请说明理由．

    分析 （Ⅰ）求利用三角形的面积公式$\frac{1}{2}$（a+c）b=$\frac{\sqrt{2}+1}{2}$，根据椭圆的离心率及a，b和c的关系，求得a与b的值，求得椭圆方程；
    （Ⅱ）当斜率存在时，设直线方程，代入椭圆方程，利用韦达定理及直线的斜率公式可知k1+k3=$\frac{{y}_{1}-t}{{x}_{1}-2}$+$\frac{{y}_{2}-t}{{x}_{2}-2}$，代入即可求得k1+k3=2t，则k2=$\frac{t}{2-1}$=t，即可求得λ的值．

    解答 解：（Ⅰ）由F1（-c，0），A（a，0），B（0，b），
    则S${\;}_{△AB{F}_{1}}$=$\frac{1}{2}$（a+c）b=$\frac{\sqrt{2}+1}{2}$，
    则（a+c）b=$\sqrt{2}$+1，即（a+c）$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{2}$+1，
    由e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，a=$\sqrt{2}$c，
    则（$\sqrt{2}$c+c）$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{2}$+1，
    解得：c=1，则a=$\sqrt{2}$，b=1，
    ∴椭圆的标准方程：$\frac{{x}^{2}}{2}+{y}^{2}=1$；
    （Ⅱ）由（Ⅰ）可知：F2的坐标为F2（1，0），设P（x1，y1），Q（x2，y2），M（2，t），
    当直线l的斜率不为0时，设l的方程为x=my+1，
    $\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$，消去x得（m2+2）y2+2my-1=0，
    则y1+y2=-$\frac{2m}{{m}^{2}+2}$，y1y2=-$\frac{1}{{m}^{2}+2}$，
    则k1+k3=$\frac{{y}_{1}-t}{{x}_{1}-2}$+$\frac{{y}_{2}-t}{{x}_{2}-2}$=$\frac{{y}_{1}-t}{m{y}_{1}-1}$•$\frac{{y}_{2}-t}{m{y}_{2}-1}$=$\frac{（{y}_{1}-t）（m{y}_{2}-1）+（{y}_{2}-t）（m{y}_{1}-1）}{（m{y}_{1}-1）（m{y}_{2}-1）}$=$\frac{2m{y}_{1}{y}_{2}-（mt+1）（{y}_{1}+{y}_{2}）+2t}{{m}^{2}{y}_{1}{y}_{2}-m（{y}_{1}+{y}_{2}）+1}$，
    =$\frac{-\frac{2m}{{m}^{2}+2}+\frac{2m（mt+1）}{{m}^{2}+2}+2t}{-\frac{{m}^{2}}{{m}^{2}+2}+\frac{2{m}^{2}}{{m}^{2}+2}+1}$，
    =$\frac{4{m}^{2}t+4t}{2{m}^{2}+2}$=2t，
    由k2=$\frac{t}{2-1}$=t，则k1+k3=2k2，
    当直线l的斜率为0时，显然k1+k3=$\frac{t}{2+\sqrt{2}}$+$\frac{t}{2-\sqrt{2}}$=2t=2k2，
    k1+k3=2k2，成立，
    综上可知：存在λ=2，使得k1+k3=λk2成立．

    点评 本题考查椭圆的标准方程及简单几何性质，考查直线与椭圆的位置关系，韦达定理，直线的斜率公式，考查计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．点M（x，y）在|x|+|y|≤2表示的平面区域内，则点M（x，y）满足x+y-1≥0的概率为0.25．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知数列{an}满足al=-2，an+1=2an+4．
    （I）证明数列{an+4}是等比数列；
    （Ⅱ）求数列{|an|}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．求函数f（x）=x+$\frac{1}{x}$-1-ln（x+3）零点的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

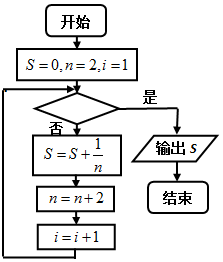    17．如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图，其中判断框内应填入的条件是（　　）
    A．i＞8B．i＞9C．i＞10D．i＞11

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．图形的对称，正弦曲线的流畅都能体现“数学美”．“黄金分割”也是数学美得 一种体现，如图，椭圆的中心在原点，F为左焦点，当$\overrightarrow{FB}⊥\overrightarrow{AB}$时，其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数g（x）=xsinθ-lnx-sinθ在[1，+∞）单调递增，其中θ∈（0，π）
    （1）求θ的值；
    （2）若$f（x）=g（x）+\frac{2x-1}{x^2}$，当x∈[1，2]时，试比较f（x）与${f^/}（x）+\frac{1}{2}$的大小关系（其中f′（x）是f（x）的导函数），请写出详细的推理过程；
    （3）当x≥0时，ex-x-1≥kg（x+1）恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=ex+ax，（a∈R），其图象与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2
    （1）求a的取值范围；
    （2）证明：$f'（\frac{{3{x_1}+{x_2}}}{4}）＜0$；（f′（x）为f（x）的导函数）
    （3）设点C在函数f（x）的图象上，且△ABC为等边三角形，记$\sqrt{\frac{x_2}{x_1}}=t$，求（t-1）（a+$\sqrt{3}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知a＞0，b＞0，c＞0，函数f（x）=|x+a|-|x-b|+c的最大值为10．
    （1）求a+b+c的值；
    （2）求$\frac{1}{4}$（a-1）2+（b-2）2+（c-3）2的最小值，并求出此时a、b、c的值．

    查看答案和解析>>

    同步练习册答案