
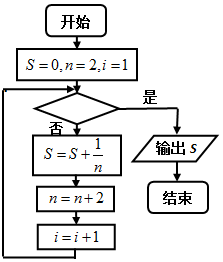
 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>8 | B. | i>9 | C. | i>10 | D. | i>11 |
分析 模拟程序框图知,程序运行后要求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的和,
由i=1时S=$\frac{1}{2}$,i=2时S=$\frac{1}{2}$+$\frac{1}{4}$,依此类推共有10项,“i>10”.
解答 解:根据题意,模拟程序框图知:
程序运行后要求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的和,
且当i=1时,S=$\frac{1}{2}$,
当i=2时,S=$\frac{1}{2}$+$\frac{1}{4}$,
依此类推,一共有10项,
因而判断框中应填“i>10”.
故选:C.
点评 本题考查了程序框图的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
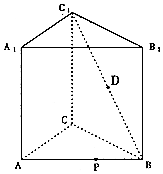 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | xy≠10是x≠5或y≠2的充分不必要条件 | |
| B. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0 | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 相关指数R2越接近1,表示残差平方和越大. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
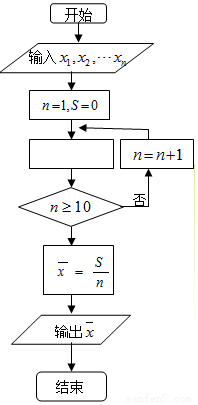 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com