
分析 由题意,A是OB的中点.设A(x1,y1),B(x2,y2).联立方程化为k2x2+(2k2-4)x+k2=0,(k>0).可得根与系数的关系,利用焦点弦与抛物线的定义可得:|FA|=x1+1,|FB|=x2+1,利用|FB|=2|FA|,联立解出即可.
解答 解:由题意,A是OB的中点.设A(x1,y1),B(x2,y2).
联立直线y=k(x+1)(k>0)与抛物线C:y2=4x,
化为k2x2+(2k2-4)x+k2=0,(k>0).
∴x1+x2=$\frac{4}{{k}^{2}}$-2①,x1x2=1②.
∵A是OB的中点,
∴|FB|=2|FA|,|FA|=x1+1,|FB|=x2+1,
∴x2+1=2(x1+1)③,
化为x2=2x1+1.
联立①②③,解得k=$\frac{2\sqrt{2}}{3}$.
故答案为$\frac{2\sqrt{2}}{3}$.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、焦点弦的性质,考查了推理能力与计算能力,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {0,1,2,3} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6x-5y-14=0 | B. | 6x-5y+14=0 | C. | 6x+5y+14=0 | D. | 6x+5y-14=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
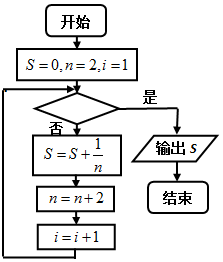 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>8 | B. | i>9 | C. | i>10 | D. | i>11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com