
分析 (I)利用极坐标方程,即可证明:|OB|+|OC|=$\sqrt{2}$|OA|;
(II)当φ=$\frac{π}{12}$时,直线l经过B,C两点,求出B,C的坐标,即可求m与α的值.
解答 (Ⅰ)证明:由已知:$|{OB}|=4cos({φ+\frac{π}{4}}),|{OC}|=4cos({φ-\frac{π}{4}}),|{OA}|=4cosφ$
∴$|{OB}|+|{OC}|=4cos({φ+\frac{π}{4}})+4cos({φ-\frac{π}{4}})=8cosφcos\frac{π}{4}=\sqrt{2}|{OA}|$…(5分)
(Ⅱ)解:当$φ=\frac{π}{12}$时,点B,C的极角分别为$φ+\frac{π}{4}=\frac{π}{3},φ-\frac{π}{4}=-\frac{π}{6}$,
代入曲线M的方程得点B,C的极径分别为:${ρ_B}=4cos\frac{π}{3}=2,{ρ_C}=4cos({-\frac{π}{6}})=2\sqrt{3}$
∴点B,C的直角坐标为:$B({1,\sqrt{3}}),C({3,-\sqrt{3}})$,
则直线l的斜率为$k=-\sqrt{3}$,方程为$l:\sqrt{3}x+y-2\sqrt{3}=0$,与x轴交与点(2,0);
由$l:\left\{\begin{array}{l}x=m+tcosα\\ y=tsinα\end{array}\right.$,知α为其倾斜角,直线过点(m,0),
∴$m=2,α=\frac{2π}{3}$…(10分)
点评 本题考查极坐标方程的运用,考查直线的参数方程,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈({0,+∞}),lnx≥2\frac{x-1}{x+1}$ | B. | $?{x_0}∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ | ||
| C. | $?x∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ | D. | 不存在${x_0}∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某几何体的三视图如图所示,则该几何体的表面积为( )
已知某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 16+3π | B. | 12+3π | C. | 8+4$\sqrt{2}$+3π | D. | 4+4$\sqrt{2}$+3π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
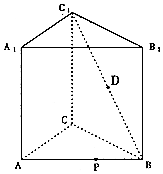 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com