
已知抛物线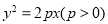 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4,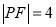 .
.
(1)求抛物线的方程;
(2)设点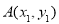 ,
,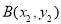 (
(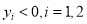 )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
(1)抛物线的方程为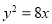 .(2)
.(2)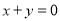 .
.
【解析】
试题分析:(1)由抛物线的定义可得一个关于点P横坐标及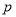 的等式,结合该点在抛物线上,因此可求得
的等式,结合该点在抛物线上,因此可求得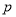 的值,即可得结论.
的值,即可得结论.
(2)由∠APB的角平分线与x轴垂直,可得PA,PB的倾斜角互补,即PA,PB的斜率互为相反数.通过假设直线PA的方程,联立抛物线方程可得到点A的坐标,根据PA,PB的斜率关系即可得对应的得到点B的坐标,由此可得到直线AB的斜率,由此可通过假设直线AB的方程联立抛物线方程,根据两点公式求出AB的长,根据点到直线的距离公式,即可表示出三角形PAB的面积,再结合函数的导数求出最值.
试题解析:(1)设 ,因为
,因为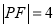 ,由抛物线的定义得
,由抛物线的定义得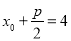 ,又
,又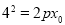 ,
,
因此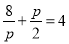 ,解得
,解得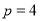 ,从而抛物线的方程为
,从而抛物线的方程为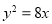 .
.
(2)由(1)知点P的坐标为P(2,4),因为∠APB的角平分线与x轴垂直,所以可知PA,PB的倾斜角互补,即PA,PB的斜率互为相反数.
设直线PA的斜率为k,则 ,由题意
,由题意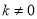 ,
,
把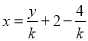 代入抛物线方程得
代入抛物线方程得 ,该方程的解为4、
,该方程的解为4、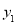 ,
,
由韦达定理得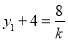 ,即
,即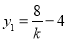 ,同理
,同理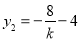 .
.
所以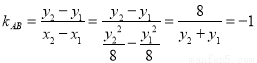 ,
,
设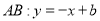 ,把
,把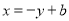 代入抛物线方程得
代入抛物线方程得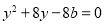 ,
,
由题意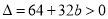 ,且
,且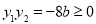 ,从而
,从而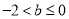
又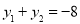 ,所以
,所以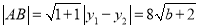 ,点P到AB的距离
,点P到AB的距离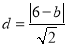 ,
,
因此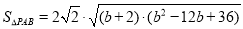 ,设
,设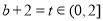 ,
,
则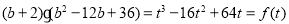 ,
,
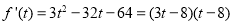
由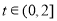 知
知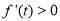 ,所以
,所以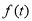 在
在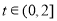 上为增函数,因此
上为增函数,因此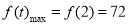 ,
,
即△PAB面积的最大值为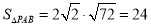 .
.
△PAB的面积取最大值时b=0,所以直线AB的方程为 .
.
考点:1. 抛物线的定义及其几何性质;2. 直线与抛物线的位置关系;3. 直线方程;4.应用导数研究函数的最值.
考点分析: 考点1:抛物线的标准方程 考点2:抛物线的几何性质 试题属性

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年陕西省宝鸡市九校高三联合检测文科数学试卷(解析版) 题型:解答题
已知某校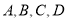 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从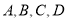 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从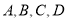 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:选择题
等差数列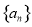 的前n项和为
的前n项和为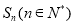 ,且满足
,且满足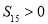 ,
,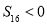 ,则
,则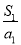 ,
,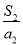 ,…,
,…, 中最大的项为( )
中最大的项为( )
A.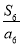 B.
B.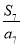 C.
C.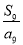 D.
D.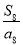
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试理科数学试卷(解析版) 题型:选择题
如下图是张大爷晨练时所走的离家距离(y)与行走时间(x)之间函数关系的图象,若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )
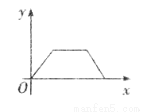
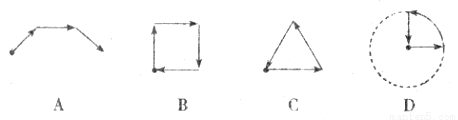
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试文科数学试卷(解析版) 题型:填空题
一枚质地均匀的正方体玩具,四个面标有数字1,其余两个面标有数字2,抛掷两次,所得向上数字相同的概率是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知数列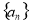 的前
的前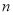 项和为
项和为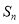 ,且满足
,且满足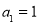 ,
, 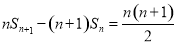 ,
, 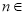 N
N .
.
(1)求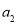 的值;
的值;
(2)求数列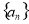 的通项公式;
的通项公式;
(3)是否存在正整数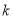 ,使
,使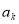 ,
, ,
, 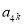 成等比数列? 若存在,求
成等比数列? 若存在,求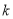 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com