练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司从1999年的年产值100万元，增加到10年后2009年的500万元，如果每年产值增长率相同，则每年的平均增长率是多少？(ln(1＋x)≈x，lg2＝0.3，ln10＝2.30)

    【答案】16.1%.

    【解析】试题分析：设每年的年产值增长率是 ，由题意可得： 化为 ，即可得出 ，解出即可得出

    试题解析：设每年年增长率为x，

    则100(1＋x)10＝500，即(1＋x)10＝5，

    两边取常用对数，得

    10·lg(1＋x)＝lg5，

    ∴lg(1＋x)＝＝ (lg10－lg2)＝.

    又∵lg(1＋x)＝，

    ∴ln(1＋x)＝lg(1＋x)·ln10.

    ∴ln(1＋x)＝×ln10＝×2.30＝0.161＝16.1%.

    又由已知条件：ln(1＋x)≈x得x≈16.1%.

    故每年的平均增长率约为16.1%.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面为矩形，D为

    的中点，AC⊥平面BCC1B1．

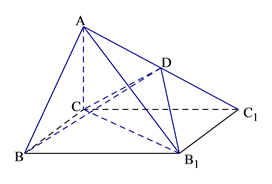
    （Ⅰ）证明：AB//平面CDB1;

    （Ⅱ）若AC=BC=1，BB1=,

    （1）求BD的长；

    （2）求三棱锥C-DB1C1的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以直角坐标系的原点为极点， 轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，点的极坐标为，圆以为圆心，4为半径；又直线的极坐标方程为。

    （Ⅰ）求直线和圆的普通方程；

    （Ⅱ）试判定直线和圆的位置关系．若相交，则求直线被圆截得的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在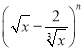的展开式中，第5项的系数与第3项的系数之比是56：3．

    （1）求展开式中的所有有理项；

    （2）求展开式中系数绝对值最大的项．

    （3）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝3ax2＋2bx＋c，a＋b＋c＝0，f(0)>0，f(1)>0，证明a>0，并利用二分法证明方程f(x)＝0在区间[0,1]内有两个实根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017长沙模拟】如图，在直棱柱ABCA1B1C1中，∠BAC＝90°，AB＝AC＝，AA1＝3，D是BC的中点，点E在棱BB1上运动．

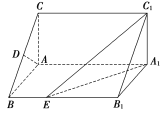
    (1)求证：AD⊥C1E；

    (2)当异面直线AC，C1E所成的角为60°时，求三棱锥C1A1B1E的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如下（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）.

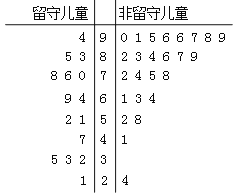
    （Ⅰ）根据茎叶图中的数据完成列联表，并判断能否有的把握认为孩子的幸福感强与是否是留守儿童有关？

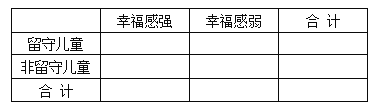
    （Ⅱ）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率.

    参考公式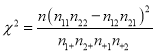： ； 附表：

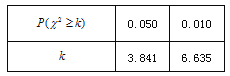
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列5个命题中正确命题的个数是( )

    ①对于命题p：x∈R，使得x2＋x＋1<0，则綈p：x∈R，均有x2＋x＋1>0；

    ②m＝3是直线(m＋3)x＋my－2＝0与直线mx－6y＋5＝0互相垂直的充要条件；

    ③已知回归直线的斜率的估计值为1.23，样本点的中心为(4,5)，则线性回归方程为＝1.23x＋0.08；

    ④若实数x，y∈[－1,1]，则满足x2＋y2≥1的概率为；

    ⑤曲线y＝x2与y＝x所围成图形的面积是S＝ (x－x2)dx.

    A．2 B．3

    C．4 D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人对东北一种松树的生长进行了研究，收集了其高度h(米)与生长时间t(年)的相关数据，选择h＝mt＋b与h＝loga(t＋1)来刻画h与t的关系，你认为哪个符合？并预测第8年的松树高度．

    t(年)

    1

    2

    3

    4

    5

    6

    h(米)

    0.6

    1

    1.3

    1.5

    1.6

    1.7

    查看答案和解析>>

    同步练习册答案