
分析 由已知利用余弦定理可求c,利用正弦定理即可求sinB,利用反三角函数即可表示出B.
解答 解:∵a=24,b=13,C=120°,
∴c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{2{4}^{2}+1{3}^{2}-2×24×13×cos120°}$=$\sqrt{1057}$.
∴由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$,可得:sinB=$\frac{bsinC}{c}$=$\frac{13×\frac{\sqrt{3}}{2}}{\sqrt{1057}}$=$\frac{13\sqrt{3171}}{2114}$,
∴B=arcsin$\frac{13\sqrt{3171}}{2114}$.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
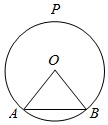 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$ | B. | 2,-2$\sqrt{2}$,4 | C. | 4,8,12 | D. | lg2,lg4,lg8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
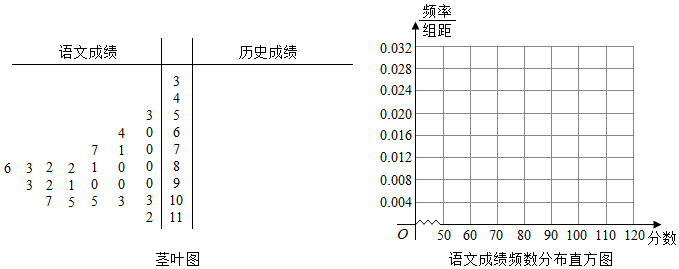
| 语文成绩分组 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
| 频数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com