
分析 由多项式的乘法展开重新组合为3+($\frac{ac}{{b}^{2}}$+$\frac{{b}^{2}}{ac}$)+($\frac{ab}{{c}^{2}}$+$\frac{{c}^{2}}{ab}$)+($\frac{bc}{{a}^{2}}$+$\frac{{a}^{2}}{bc}$),三个括号同时用基本不等式可得.
解答 解:∵a,b,c∈R+,∴($\frac{a}{b}$+$\frac{b}{c}$+$\frac{c}{a}$)($\frac{b}{a}$+$\frac{c}{b}$+$\frac{a}{c}$)
=1+$\frac{ac}{{b}^{2}}$+$\frac{{a}^{2}}{bc}$+$\frac{{b}^{2}}{ac}$+1+$\frac{ab}{{c}^{2}}$+$\frac{bc}{{a}^{2}}$+$\frac{{c}^{2}}{ab}$+1
=3+($\frac{ac}{{b}^{2}}$+$\frac{{b}^{2}}{ac}$)+($\frac{ab}{{c}^{2}}$+$\frac{{c}^{2}}{ab}$)+($\frac{bc}{{a}^{2}}$+$\frac{{a}^{2}}{bc}$)
≥3+2$\sqrt{\frac{ac}{{b}^{2}}•\frac{{b}^{2}}{ac}}$+2$\sqrt{\frac{ab}{{c}^{2}}•\frac{{c}^{2}}{ab}}$+2$\sqrt{\frac{bc}{{a}^{2}}•\frac{{a}^{2}}{bc}}$=9
当且仅当$\frac{ac}{{b}^{2}}$=$\frac{{b}^{2}}{ac}$且$\frac{ab}{{c}^{2}}$=$\frac{{c}^{2}}{ab}$且$\frac{bc}{{a}^{2}}$=$\frac{{a}^{2}}{bc}$即a=b=c时,
原式取到最小值9
故答案为:9
点评 本题考查基本不等式求最值,变形为可用基本不等式的形式是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:填空题
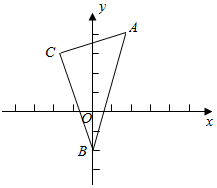 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 2+$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生长指数 | 2 | 1 | 0 | -1 | ||
| 地域 | 南区 | 空气质量好 | 45 | 54 | 26 | 35 |
| 空气质量差 | 7 | 16 | 12 | 5 | ||
| 北区 | 空气质量好 | 70 | 105 | 20 | 25 | |
| 空气质量差 | 19 | 38 | 18 | 5 | ||
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com