
分析 仔细阅读题目便可发现存留污垢y是以a为首项,以$\frac{1}{3}$为公比的等比数列,利用等比数列的通项公式,列出漂洗次数n与存留污垢y的关系式,解不等式便可得出答案.
解答 解:设原有污垢为为a,漂洗n次后,存留污垢为y,
由题意可知:漂洗一次后存留污垢y1=(1-$\frac{2}{3}$)a=$\frac{1}{3}$a,
漂洗两次后存留污垢y2=(1-$\frac{2}{3}$)2a=($\frac{1}{3}$)2a,
…
漂洗n次后存留污垢yn=(1-$\frac{2}{3}$)na=($\frac{1}{3}$)na,
若使存留的污垢不超过原有的2%,
则有yn=($\frac{1}{3}$)na≤2%•a,
解不等式得n≥4,
故该洗衣机至少要清洗的次数为4次.
故答案为:4.
点评 本题考查了等比数列的通项公式,考查了学生的审题及建模能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
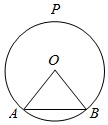 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$ | B. | 2,-2$\sqrt{2}$,4 | C. | 4,8,12 | D. | lg2,lg4,lg8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{7}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com