
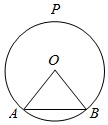
 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.分析 (1)求出O到AB和CD的距离,AB与CD的长,代入梯形面积公式,可得S关于α的函数关系;
(2)结合正弦函数的图象和性质及二次函数的图象和性质,可得S的最大值及最大值点.
解答 解:(1)如下图所示: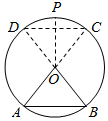
∵圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=2,O到AB的距离d=1,
若∠POD=α,则CD=2$\sqrt{2}$sinα,O到CD的距离h=$\sqrt{2}$cosα,
故S=$\frac{1}{2}$(2$\sqrt{2}$sinα+2)($\sqrt{2}$cosα+1)
=2sinαcosα+$\sqrt{2}$(sinα+cosα)+1
=(sinα+cosα)2+$\sqrt{2}$(sinα+cosα)
=2sin2(α+$\frac{π}{4}$)+2sin(α+$\frac{π}{4}$).
(2)令t=sin(α+$\frac{π}{4}$).则S=2t2+2t,t∈[$\frac{\sqrt{2}}{2}$,1],
∵S=2t2+2t的图象是开口朝上,且以直线t=-$\frac{1}{2}$为对称的抛物线,
故当t=1,即α=$\frac{π}{4}$时,S取最大值4.
点评 本题主要考查了函数的解析式的求法,函数的最值及其几何意义,二次函数的图象和性质,正弦函数的图象和性质,考查了数形结合思想和转化思想的应用,考查了计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
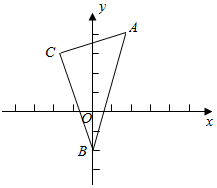 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生长指数 | 2 | 1 | 0 | -1 | ||
| 地域 | 南区 | 空气质量好 | 45 | 54 | 26 | 35 |
| 空气质量差 | 7 | 16 | 12 | 5 | ||
| 北区 | 空气质量好 | 70 | 105 | 20 | 25 | |
| 空气质量差 | 19 | 38 | 18 | 5 | ||
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com