
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由条件即可得出$S=2{\overrightarrow{a}}^{2}+3{\overrightarrow{b}}^{2}$,或${\overrightarrow{a}}^{2}+2{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$,或${\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}$,先可判断①错误,而$\overrightarrow{a}⊥\overrightarrow{b}$时,便可得出${S}_{min}={\overrightarrow{b}}^{2}$,从而判断出②正确,$\overrightarrow{a}∥\overrightarrow{b}$时,可设$\overrightarrow{b}=k\overrightarrow{a}$,从而可判断③错误,而$|\overrightarrow{b}|=4|\overrightarrow{a}|$时,可以求出${S}_{min}=16{\overrightarrow{a}}^{2}+16{\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>>0$,从而判断出④正确,而$|\overrightarrow{b}|=2|\overrightarrow{a}|$,且${S}_{min}=8|\overrightarrow{a}{|}^{2}$时,可以求出$\overrightarrow{a},\overrightarrow{b}$夹角为$\frac{π}{3}$,或$\frac{2π}{3}$,从而判断说法⑤错误,从而找出正确选项.
解答 解:根据条件得,$S=2{\overrightarrow{a}}^{2}+3{\overrightarrow{b}}^{2}$,或${\overrightarrow{a}}^{2}+2{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$,或${\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}$;
∴①错误;
$\overrightarrow{a}⊥\overrightarrow{b}$时,$\overrightarrow{a}•\overrightarrow{b}=0$,∴${S}_{min}={\overrightarrow{b}}^{2}$;
即Smin与$|\overrightarrow{a}|$无关;
∴②正确;
若$\overrightarrow{a}∥\overrightarrow{b}$,设$\overrightarrow{a}=k\overrightarrow{b}$,则S=$(2{k}^{2}+3){\overrightarrow{b}}^{2}$,或$({k}^{2}+2+2k){\overrightarrow{b}}^{2}$,或$(1+4k){\overrightarrow{b}}^{2}$;
∴Smin与$|\overrightarrow{b}|$有关;
∴③错误;
若$|\overrightarrow{b}|>4|\overrightarrow{a}|$,当$|\overrightarrow{b}|=4|\overrightarrow{a}|$时,S=$50{\overrightarrow{a}}^{2}$,或${\overrightarrow{a}}^{2}+32{\overrightarrow{a}}^{2}+8{\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>$,或$16{\overrightarrow{a}}^{2}+16{\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>$;
∴Smin>0;
∴④正确;
若$|\overrightarrow{b}|=2|\overrightarrow{a}|$,则$S=14{\overrightarrow{a}}^{2}$,或$8{\overrightarrow{a}}^{2}+{\overrightarrow{a}}^{2}{+2\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>$,或$4{\overrightarrow{a}}^{2}+8{\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>$;
∴${S}_{min}=8|\overrightarrow{a}{|}^{2}$时,${\overrightarrow{a}}^{2}+2{\overrightarrow{a}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>=0$,或$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$\overrightarrow{a}$,$\overrightarrow{b}$夹角为$\frac{2π}{3}$或$\frac{π}{3}$;
∴⑤错误;
故说法正确的有2个.
故选B.
点评 考查向量数量积的运算及计算公式,向量垂直的充要条件,共线向量基本定理,以及向量夹角的范围.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
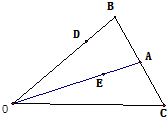 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com