
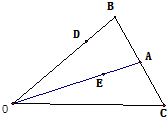
 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.分析 (1)由平面向量的加法法则能用向量$\overrightarrow{a}$与$\overrightarrow{b}$表示向量$\overrightarrow{OC},\overrightarrow{CD}$.
(2)由$\overrightarrow{CE}=\overrightarrow{CO}+\overrightarrow{OE}=a+b+\frac{3}{5}({-b})=a+\frac{2}{5}b$,能求出C、D、E三点不共线.
解答 解:(1)∵$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
∴$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{AC}$=-$\overrightarrow{a}-\overrightarrow{b}$,
$\overrightarrow{CD}$=$\overrightarrow{CB}$+$\overrightarrow{BD}$=$\overrightarrow{CB}$+$\frac{1}{3}$$\overrightarrow{BO}$=$\overrightarrow{CB}$+$\frac{1}{3}$($\overrightarrow{BA}$+$\overrightarrow{AO}$)
=2$\overrightarrow{a}$+$\frac{1}{3}$(-$\overrightarrow{a}+\overrightarrow{b}$)
=$\frac{5}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$,
(2)∵$\overrightarrow{CE}=\overrightarrow{CO}+\overrightarrow{OE}=a+b+\frac{3}{5}({-b})=a+\frac{2}{5}b$,
∴$不存在实数λ,满足\overrightarrow{CE}=λ\overrightarrow{CD}$,
∴C、D、E三点不共线.
点评 本题考查向量的求法,考查三点是否共线的判断,是中档题,解题时要认真审题,注意平面向量的运算法则的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | a<1 | B. | a≥1 | C. | b≤1 | D. | b≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
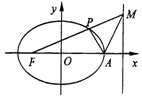 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.
河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ③④ | D. | 都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com