
| A. | ①② | B. | ①④ | C. | ③④ | D. | 都不正确 |
分析 利用对数的运算性质即可判断出正误.
解答 解:利用对数的运算性质可得:①$lo{g}_{a}(x{y}^{2})$=logax+2logay,因此①不正确;
②$lo{g}_{a}(x\sqrt{y})$=logax+$\frac{1}{2}$logay,因此②不正确;
③$lo{g}_{a}\frac{xy}{{z}^{3}}$=logax+logay-3logaz,因此③不正确;
④$lo{g}_{a}\frac{\sqrt{xy}}{z}$=$\frac{1}{2}$logax+$\frac{1}{2}$logay-logaz,因此④不正确.
综上:都不正确.
故选:D.
点评 本题考查了对数的运算性质,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
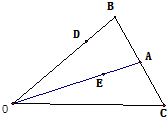 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<0 | B. | $-\frac{3}{4}<a<0$ | C. | $-\frac{3}{2}≤a<0$ | D. | $-\frac{3}{4}≤a<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com