
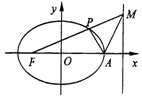
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.分析 (1)由椭圆的离心率e=$\frac{c}{a}$=$\frac{2}{3}$,准线方程x=$\frac{{a}^{2}}{c}$=$\frac{9}{2}$,即可求得a和c的值,则b2=a2-c2=5,即可求得椭圆C的标准方程;
(2)由∠FPA为直角,以AF为直径的圆的与椭圆相交于P点,设P(x,±$\sqrt{5(1-\frac{{x}^{2}}{9})}$),求得圆心为O($\frac{1}{2}$,0)及半径为$\frac{5}{2}$,根据点到直线的距离公式,即可求得a的值,代入求得y的值,即可求得P点坐标;
(3)设点P(x1,y1)(-2<x1<3),点M$M({\frac{9}{2},{y_2}})$,由点F、P、M三点共线,求得点M的坐标,$M({\frac{9}{2},\frac{{13{y_1}}}{{2({{x_1}+2})}}})$.${k_1}=\frac{y_1}{{{x_1}-3}},{k_2}=\frac{{13{y_1}}}{{3({{x_1}+2})}}$,则${k_1}•{k_2}=\frac{{-13•\frac{5}{9}({x_1^2-9})}}{{3({{x_1}+2})({{x_1}-3})}}=-\frac{65}{27}•\frac{{{x_1}+3}}{{{x_1}+2}}=-\frac{65}{27}({1+\frac{1}{{{x_1}+2}}})$.由此可导出k1•k2的取值范围.
解答 解:(1)由题意可知:离心率e=$\frac{c}{a}$=$\frac{2}{3}$,
准线方程x=$\frac{{a}^{2}}{c}$=$\frac{9}{2}$,
解得:a=3,c=2,
由b2=a2-c2=5,
∴求椭圆C的标准方程为$\frac{x^2}{9}+\frac{y^2}{5}=1$;…(4分)
(2)由∠FPA为直角,
∴以AF为直径的圆的与椭圆相交于P点,设P(x,±$\sqrt{5(1-\frac{{x}^{2}}{9})}$),
∴圆心为O($\frac{1}{2}$,0),半径为$\frac{5}{2}$,
∴丨PO丨=$\frac{5}{2}$,即$\sqrt{(x-\frac{1}{2})^{2}+5(1-\frac{{x}^{2}}{9})}$=$\frac{5}{2}$,整理得:4x2-9x-9=0,
解得:x=-$\frac{3}{4}$或x=3(舍去),
∴y=±$\sqrt{5(1-\frac{{x}^{2}}{9})}$=±$\frac{5\sqrt{3}}{4}$,
∴P点坐标为:$({-\frac{3}{4},±\frac{{5\sqrt{3}}}{4}})$…(8分)
(3)设点P(x1,y1)(-2<x1<3),点$M({\frac{9}{2},{y_2}})$,
∵点F,P,M共线,x1≠-2,
∴$\frac{y_1}{{{x_1}+2}}=\frac{y_2}{{\frac{13}{2}}}$,即${y_2}=\frac{{13{y_1}}}{{2({{x_1}+2})}}$,
∴$M({\frac{9}{2},\frac{{13{y_1}}}{{2({{x_1}+2})}}})$,…(10分)
∵${k_1}=\frac{y_1}{{{x_1}-3}},{k_2}=\frac{{13{y_1}}}{{3({{x_1}+2})}}$,
∴${k_1}•{k_2}=\frac{y_1}{{{x_1}-3}}•\frac{{13{y_1}}}{{3({{x_1}+2})}}=\frac{13y_1^2}{{3({{x_1}+2})({{x_1}-3})}}$,…(12分)
又∵点P在椭圆C上,
∴$y_1^2=-\frac{5}{9}({x_1^2-9})$,
∴${k_1}•{k_2}=\frac{{-13•\frac{5}{9}({x_1^2-9})}}{{3({{x_1}+2})({{x_1}-3})}}=-\frac{65}{27}•\frac{{{x_1}+3}}{{{x_1}+2}}=-\frac{65}{27}({1+\frac{1}{{{x_1}+2}}})$,…(14分)
∵-2<x1<3,
∴${k_1}•{k_2}<-\frac{26}{9}$,
故k1•k2的取值范围为$({-∞,-\frac{26}{9}})$…(16分)
点评 本题考查椭圆的标准方程及简单几何性质,直线的圆锥曲线的位置关系,考查圆的方程及点到直线的距离公式,直线的斜率公式,考查计算能力,解题时要认真审题,属于中档题.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
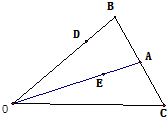 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com