
分析 ?x>0,$\frac{x}{(x+1)^{2}}$≤a恒成立,即函数f(x)=$\frac{x}{(x+1)^{2}}$的最大值小于等于a,利用导数当研究函数的最值,可得答案.
解答 解:∵对于?x>0,$\frac{x}{(x+1)^{2}}$≤a恒成立,
故函数f(x)=$\frac{x}{(x+1)^{2}}$的最大值小于等于a,
∵f′(x)=$\frac{1-{x}^{2}}{{(x+1)}^{4}}$,
故当x<-1时,f′(x)<0,函数f(x)为减函数,且恒为负,
当-1<x≤1时,f′(x)≥0,函数f(x)为增函数,且恒为正,
当x>1时,f′(x)<0,函数f(x)为减函数,且恒为正,
即x=1时,函数有最大值$\frac{1}{4}$
故a的取值范围是:[$\frac{1}{4}$,+∞),
故答案为:[$\frac{1}{4}$,+∞).
点评 本题以命题的真假判断与应用为载体,考查了全称命题,函数恒成立,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(2a) | B. | f(a2)<f(a) | C. | f(a2+a)<f(a) | D. | f(a2+1)>f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
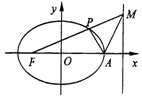 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为$\frac{2}{3}$,点M的横坐标为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.
河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com