
 河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.
河大校办工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机抽取100件测量它们的直径,得到如图所示的频率分布直方图.分析 (1)利用所有小矩形的面积之和为1求得a值;根据频数=频率×样本容量求得各组的频数,代入平均数公式计算;
(2)根据频率分布直方图求得直径位于区间[112,114)和[114,116)的频率之比,可得在两组中应取的产品数,利用写出所有基本事件的方法求符合条件的基本事件个数比.
解答 解:(1)由频率分布直方图得:2×(0.050+0.150+a+0.075)=1⇒a=0.225,
直径位于区间[110,112)的频数为100×2×0.050=10,位于区间[112,114)的频数为100×2×0.150=30,
位于区间[114,116)的频数为100×2×0.225=45,位于区间[116,118)的频数为100×2×0.075=15,
∴生产一件A产品的平均利润为$\frac{10×10+20×30+30×45+10×15}{100}$=22(元) …(6分)
(2)由频率分布直方图得:直径位于区间[112,114)和[114,116)的频率之比为2:3,
∴应从直径位于区间[112,114)的产品中抽取2件产品,记为A、B,
从直径位于区间[114,116)的产品中抽取3件产品,记为a、b、c,从中随机抽取两件,所有可能的取法有(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(a,b),(a,c),(b,c)10种,其中两件产品中至少有一件产品的直径位于区间[112,114)内的取法有(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c)共7种.
∴所求概率为$P=\frac{7}{10}$…(12分)
点评 本题考查了分层抽样方法,考查了古典概型的概率计算,读懂频率分布直方图是解答本题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
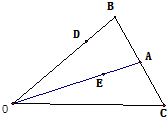 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近B的三等分点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AO}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<0 | B. | $-\frac{3}{4}<a<0$ | C. | $-\frac{3}{2}≤a<0$ | D. | $-\frac{3}{4}≤a<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
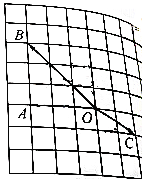 在如图所示的方格纸中,用直尺和圆规画出下列向量:
在如图所示的方格纸中,用直尺和圆规画出下列向量:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com