
分析 (1)由调件利用y=Asin(ωx+φ)的图象变换规律,求得函数f(x)的表达式.
(2)由条件利用正弦函数的周期性,正弦函数的图象的对称性,得出结论.
(3)由条件利用正弦函数的定义域和值域,求得函数f(x)的最小值.
解答 解:(1)把函数y=msinx(其中m≠0)的图象上的所有点向左平移$\frac{π}{6}$个单位,
可得y=msin(x+$\frac{π}{6}$)的图象;
再将所得图象上所有点的横坐标压缩到原来的$\frac{1}{2}$倍,纵坐标保持不变,
得到了函数y=f(x)=msin(2x+$\frac{π}{6}$)的图象,故f(x)=msin(2x+$\frac{π}{6}$).
(2)当m=$\frac{1}{2}$时,函数f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{6}$),它的最小正周期为$\frac{2π}{2}$=π,
令2x+$\frac{π}{6}$=kπ,求得x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,可得它的图象的对称中心为($\frac{kπ}{2}$-$\frac{π}{12}$,0),k∈Z.
(3)若x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
函数f(x)=msin(2x+$\frac{π}{6}$)的最大值为|m|=2,∴m=±2.
若m=2,函数f(x)=2sin(2x+$\frac{π}{6}$)的最小值为f(-$\frac{π}{6}$)=2•(-$\frac{1}{2}$)=-1;
若m=-2,函数f(x)=-2sin(2x+$\frac{π}{6}$)的最小值为f($\frac{π}{6}$)=-2•1=-2.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性以及定义域和值域,正弦函数的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a>0,b>0,c≥0. | B. | a>0,b<0,c≤0 | C. | a<0,b>0,c≥0 | D. | a<0,b<0,c≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
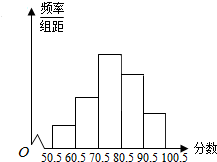 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
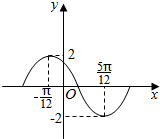
| A. | A=2,ω=2,φ=$\frac{π}{3}$ | B. | A=2,ω=2,φ=$\frac{2π}{3}$ | C. | A=2,ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ | D. | A=2,ω=2,φ=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 6 | 7 | 3 | 1 |
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一年级 | 二年级 | 三年级 | |
| 男生 | A | B | C |
| 女生 | X | Y | Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com