
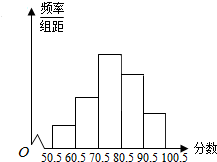
 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.分析 (1)图中矩形面积最大的一组就是人数最多的组,由此找出最高的矩形,在[70.5,80.5)这一组,再用公式求出其频数、频率;
(2)用样本估计总体:在样本中算出四个组占总数的百分比,就可以估计出成绩高于60分的学生占总人数的百分比.
解答 解:(1)最右边一组的频数是6,从左到右各小组的长方形的高之比为1:3:6:4:2
∴设样本容量为n,得(1+3+6+4+2):n=2:6
∴n=48,样本容量为48,
成绩落在[70.5,80.5)内人数最多,
频数为$6×\frac{6}{2}=18$,频率为$\frac{18}{48}$=0.375.
(2)成绩高于60(分)的学生占总人数的$\frac{3+6+4+2}{1+3+6+4+2}$=$\frac{15}{16}$=93.75%.
点评 本题考查了频率直方图的有关知识,属于基础题.频率直方图中,各个小长方形的面积等于该组数据的频率,所有长方形的面积之和等于1.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3] | B. | (-∞,3] | C. | [3,+∞) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com