
分析 (1)把已知数列递推式变形,利用累加法求得数列的通项公式;
(2)把已知数列递推式变形,利用累积法求得数列的通项公式;
(3)把已知递推式两边同时除以3n,然后得到数列{$\frac{{a}_{n}}{{3}^{n}}$}是以$\frac{{a}_{1}}{3}=\frac{1}{3}$为首项,以1为公差的等差数列,由此求得数列{an}的通项公式.
解答 解:(1)由an+1=an+n+1,得an+1-an=n+1,又a1=1,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+(n-2)+…+1=$\frac{n(n+1)}{2}$;
(2)由an+1=2n•an,得$\frac{{a}_{n+1}}{{a}_{n}}={2}^{n}$,又a1=1,
∴${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}…\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$
=2n-1•2n-2…2=21+2+…+(n-1)=${2}^{\frac{n(n-1)}{2}}$;
(3)由an=3an-1+3n(n≥2),
得$\frac{{a}_{n}}{{3}^{n}}=\frac{{a}_{n-1}}{{3}^{n-1}}+1$,即$\frac{{a}_{n}}{{3}^{n}}-\frac{{a}_{n-1}}{{3}^{n-1}}=1$(n≥2),
∴数列{$\frac{{a}_{n}}{{3}^{n}}$}是以$\frac{{a}_{1}}{3}=\frac{1}{3}$为首项,以1为公差的等差数列,
则$\frac{{a}_{n}}{{3}^{n}}=\frac{1}{3}+1×(n-1)=n-\frac{2}{3}$,
∴${a}_{n}=(n-\frac{2}{3})•{3}^{n}$.
故答案为:(1)$\frac{n(n+1)}{2}$;(2)${2}^{\frac{n(n-1)}{2}}$;(3)$(n-\frac{2}{3})•{3}^{n}$.
点评 本题考查数列递推式,考查了累加法、累积法及构造等差数列求数列的通项公式,是中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
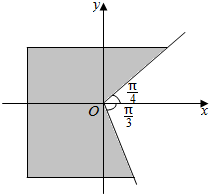
| A. | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B. | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$,k∈Z} | D. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0,b>0,c≥0. | B. | a>0,b<0,c≤0 | C. | a<0,b>0,c≥0 | D. | a<0,b<0,c≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
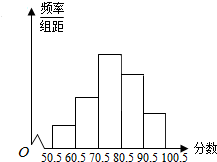 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com