
分析 利用:两个集合“保序同构”的定义,能够找出存在一个从S到T的函数y=f(x)即可判断出结论.
解答 解:①由于不存在一个从S到T的函数y=f(x),因此不是“保序同构”的集合对.
②令f(x)=x+1,x∈S=N,f(x)∈T;
③取f(x)=$\frac{9}{2}$x-$\frac{7}{2}$,x∈S,f(x)∈T,“保序同构”的集合对;
④取f(x)=tan$(πx-\frac{π}{2})$,x∈S,f(x)∈T.
综上可得:“保序同构”的集合对的序号是②③④.
故答案为:②③④.
点评 本题考查了两个集合“保序同构”的定义、函数的解析式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (x-3)2+(y-2)2=5 | B. | (x+3)2+(y-2)2=5 | C. | (x-3)2+(y-2)2=25 | D. | (x+3)2+(y-2)2=25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
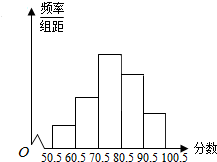 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
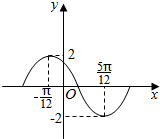
| A. | A=2,ω=2,φ=$\frac{π}{3}$ | B. | A=2,ω=2,φ=$\frac{2π}{3}$ | C. | A=2,ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ | D. | A=2,ω=2,φ=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 6 | 7 | 3 | 1 |
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (2,4) | C. | (4,2) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com