
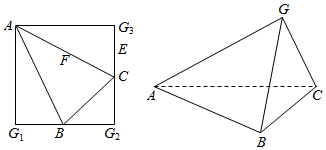
分析 (1)根据折叠前后折痕一侧的角不发生变化可知∠AGB=∠AGC=∠BGC=90°,
(2)根据AG⊥GB,AG⊥GC可得AG⊥平面GBC,故而AG⊥BC;
(3)连结EF,则EF∥AG,故而EF⊥平面GBC,所以平面EFB⊥平面GBC.
解答 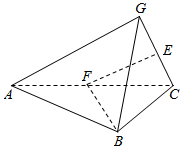 解:(Ⅰ) 在正方形AG1G2G3中,∠G1,∠G2,∠G3都是直角.
解:(Ⅰ) 在正方形AG1G2G3中,∠G1,∠G2,∠G3都是直角.
沿AB,BC及AC把这个正方形折成四面体GABC后,此三个角度数不变.
即 在四面体GABC的四个面中,
在△AGB中,∠AGB=90°,
在△AGC中,∠AGC=90°,
在△BGC中,∠BGC=90°,△ABC不是直角三角形.
故 分别在平面AGB,平面AGC和平面BGC的三角形是直角三角形.
(Ⅱ)在四面体GABC的直观图中标出点E,F
证明:因为在△AGC中,点E,F分别是GC,AC的中点,
所以EF∥AG,
因为EF?平面ABG,AG?平面ABG,
所以EF∥平面ABG.
(Ⅲ)证明:在四面体GABC中,∠AGB=90°,∠AGC=90°,
即 AG⊥GB,AG⊥GC,
因为在平面BGC中,GB∩GC=G
所以AG⊥平面BGC.
由(Ⅱ)已证EF∥AG,
所以EF⊥平面BGC.
因为EF?平面EFB
所以平面EFB⊥平面GBC.
点评 本题考查了线面垂直的判定与性质,面面垂直的判定,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0,b>0,c≥0. | B. | a>0,b<0,c≤0 | C. | a<0,b>0,c≥0 | D. | a<0,b<0,c≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
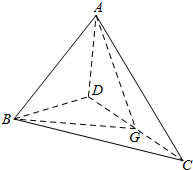
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
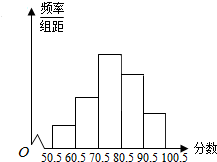 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com