
【题目】已知函数![]() ,(其中
,(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增;(2)
上单调递增;(2)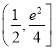 .
.
【解析】
(1)求出导数![]() ,分成
,分成![]() ,
,![]() 两种情况求导数为零的根,从而可探究出函数和导数随自变量的变化情况.
两种情况求导数为零的根,从而可探究出函数和导数随自变量的变化情况.
(2)求出![]() ,通过导数求出
,通过导数求出![]() 的单调性,结合零点存在定理得出存在
的单调性,结合零点存在定理得出存在![]() ,使得
,使得![]() ,即
,即![]() ,从而得出
,从而得出![]() 的单调性,进而求出
的单调性,进而求出![]() 的解析式,再利用
的解析式,再利用![]() 的单调性,从而可求其值域.
的单调性,从而可求其值域.
(1)解:![]() ,令
,令![]() ,当
,当![]() 时,
时,![]() 恒成立,此时
恒成立,此时![]() 单调递增;
单调递增;
当![]() 时,解
时,解![]() 得,
得,![]() ,则
,则![]() 随
随![]() 的变化如下表,
的变化如下表,
|
|
|
|
|
|
|
|
|
|
|
则![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增.
上递增.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增.
上单调递增.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,
则![]() ,设
,设![]() ,
,
则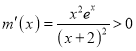 ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
对于![]() ,因为
,因为![]() ,
,![]() ,因此存在
,因此存在![]() ,
,
使得![]() ,即
,即![]() ,故
,故![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增.则
单调递增.则![]()
即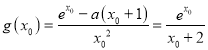 ,则
,则![]() ,由
,由 ,
,
可知,![]() 单调递增.由
单调递增.由![]() 得,
得,![]() .
.
所以![]() 的值域为
的值域为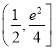 .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求
,求![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 恰有4个公共点,求
恰有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,点P是上底面A1B1C1D1内一点,且AP∥平面EFDB,则cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为2的正方形.
是边长为2的正方形.![]() 平面
平面![]() ,且
,且![]() .
.
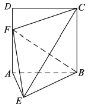
(1)求证:平面![]() 平面
平面![]() .
.
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 的高
的高![]() 若存在,请求出
若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
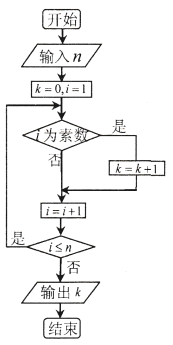
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,且满足
,且满足![]() ,以
,以![]() 为中点的线段的两端点分别为
为中点的线段的两端点分别为![]() ,其中
,其中![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 上,则
上,则![]() _______,
_______,![]() 的最小值为____________
的最小值为____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由四棱柱![]() 截去三棱锥
截去三棱锥![]() 后得到的几何体如图所示,四边形
后得到的几何体如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() .
.
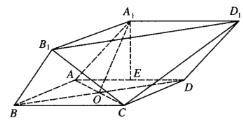
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心点O后转向东北方向(即![]() ).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
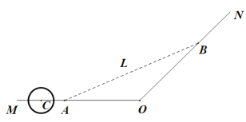
(1)求两站点A,B之间距离的最小值;
(2)公路MO段上距离市中心O30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.则如何在古建筑群C和市中心O之间设计出入口A,才能使高架道路L及其延伸段不经过保护区(不包括临界状态)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com