
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,点P是上底面A1B1C1D1内一点,且AP∥平面EFDB,则cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连结AC、BD,交于点O,连结A1C1,交EF于M,连结OM,则AO![]() PM,从而A1P=C1M,由此能求出cos∠APA1的值.
PM,从而A1P=C1M,由此能求出cos∠APA1的值.
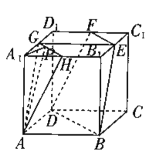
解:如图,连结AC、BD,交于点O,连结A1C1,交EF于M,连结OM,
![]()
![]() 面
面![]() ,
,![]() 为底面A1B1C1D1内一点,
为底面A1B1C1D1内一点,
∴cos∠APA1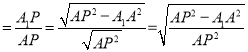
![]() ,
,
所以当![]() 取最小值时,cos∠APA1有最小值,
取最小值时,cos∠APA1有最小值,
且E,F分别为B1C1,C1D1的中点,分别取![]() 和
和![]() 的中点
的中点![]() ,
,![]() ,
,
则有![]() ,进而得到
,进而得到![]() 面
面![]() ,又
,又![]() AP∥平面EFDB,则
AP∥平面EFDB,则![]() 点必在
点必在![]() 上,
上,
明显地,当![]() 点在
点在![]() 上时,
上时,![]() 取最小值,此时
取最小值,此时![]() 取最小值,cos∠APA1有最小值,,此时,如下图,
取最小值,cos∠APA1有最小值,,此时,如下图,
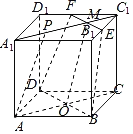
设正方形ABCD﹣A1B1C1D1中棱长为1,∵在正方形ABCD﹣A1B1C1D1中,
E,F分别为B1C1,C1D1的中点,又![]() 点P是底面A1B1C1D1内一点,
点P是底面A1B1C1D1内一点,
且AP∥平面EFDB,且面![]()
![]() 面
面![]() 于
于![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,![]() 四边形
四边形![]() 为平行四边形
为平行四边形
∴AO![]() PM,又
PM,又![]() E,F分别为B1C1,C1D1的中点,
E,F分别为B1C1,C1D1的中点,![]() ,且
,且![]() ,
,
![]() ,又
,又![]() ,∴A1P=C1M
,∴A1P=C1M![]() ,
,
∴cos∠APA1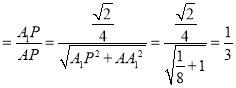 ,即cos∠APA1的最小值是
,即cos∠APA1的最小值是![]() .
.
故选:C.


科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
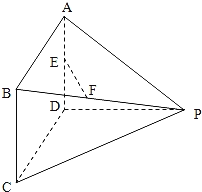
(Ⅰ)试确定点F的位置,使得直线EF∥平面PDC;
(Ⅱ)若PB=3BF,求直线AF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点为
的焦点为![]() ,准线与
,准线与![]() 轴的交点为
轴的交点为![]() .过点
.过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,当
两点,当![]() 轴时,
轴时,![]() .
.
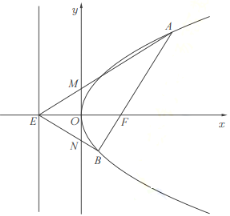
(1)求抛物线的方程;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,
,![]() 分别是其左、右焦点,过
分别是其左、右焦点,过![]() 的直线l与椭圆C交于A,B两点,且椭圆C的离心率为
的直线l与椭圆C交于A,B两点,且椭圆C的离心率为![]() ,
,![]() 的内切圆面积为
的内切圆面积为![]() ,
,![]() .
.
(I)求椭圆C的方程;
(II)若![]() 时,求直线l的方程
时,求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:

(1)将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
会员等级 | 消费金额 |
普通会员 | 2000 |
银卡会员 | 2700 |
金卡会员 | 3200 |
预计去年消费金额在![]() 内的消费者今年都将会申请办理普通会员,消费金额在
内的消费者今年都将会申请办理普通会员,消费金额在![]() 内的消费者都将会申请办理银卡会员,消费金额在
内的消费者都将会申请办理银卡会员,消费金额在![]() 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案 1:按分层抽样从普通会员, 银卡会员, 金卡会员中总共抽取 25 位“幸运之星”给予奖励: 普通会员中的“幸运之星”每人奖励 500 元; 银卡会员中的“幸运之星”每人奖励 600 元; 金卡会员中的“幸运之星”每人奖励 800 元.
方案 2:每位会员均可参加摸奖游戏,游戏规则如下:从-个装有 3 个白球、 2 个红球(球只有颜色不同)的箱子中, 有放回地摸三次球,每次只能摸-个球.若摸到红球的总数消费金额/元为 2,则可获得 200 元奖励金; 若摸到红球的总数为 3,则可获得 300 元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏;每位银卡会员均可参加 2 次摸奖游戏;每位金卡会员均可参加 3 次摸奖游戏(每次摸奖的结果相互独立) .
以方案 2 的奖励金的数学期望为依据,请你预测哪-种方案投资较少?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com