
(本小题满分12分)求证:32n+2-8n–9(n∈N*)能被64整除.
方法1:二项式定理
证明:32n+2-8n–9=9n+1-8n–9=(8+1)n+1-8n–9 ………………………………4分
=8n+1+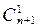 ·8n+…+
·8n+…+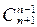 ·82+
·82+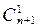 ·8+
·8+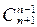 -8n-9
-8n-9
=82(8n-1+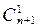 8n-2+…+
8n-2+…+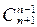 )+8(n+1)+1-8n-9…………………8分
)+8(n+1)+1-8n-9…………………8分
=64(8n-1+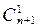 8n-2+…+
8n-2+…+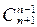 ) …………………………………10分
) …………………………………10分
∵8n-1+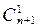 8n-2+…+
8n-2+…+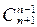 ∈Z,
∈Z,
∴32n+2-8n–9能被64整除. …………………………………12分
方法2:数学归纳法
(1)当n=1时,式子32n+2-8n–9=34-8-9=64能被64整除,命题成立.………………2分
(2)假设当n=k时,32k+2-8k-9能够被64整除. ………………………………4分
当n=k+1时,
32k+4-8(k+1)-9
=9[32k+2-8k-9]+64k+64
=9[32k+2-8k-9]+64(k+1) …………………………………8分
因为32k+2-8k-9能够被64整除,
∴9[32k+2-8k-9]+64(k+1)能够被64整除. …………………………………10分
即当n=k+1时,命题也成立.
由(1)(2)可知,32n+2-8n–9(n∈N*)能被64整除.……………………………12分
解析


科目:高中数学 来源: 题型:解答题
某中学的高二(1)班有男同学45名,女同学15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组。求某同学被抽到的概率及课外兴趣小组中男、女同学的人数。
经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出一名同学做实验,该同学做完后再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率。
实验结束后,第一次做实验的同学得到的实验数据为68,70,71,72,74.第二次做实验的同学得到的实验数据为69,70,70,72,74.请问哪位同学的实验更稳定?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率;
(Ⅱ)求笼内至少剩下5只果蝇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆的方程
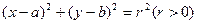 ,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径。问:
,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径。问:
(1)可以作多少个不同的圆?
(2)经过原点的圆有多少个?
(3)圆心在直线上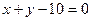 的圆有多少个?
的圆有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)现有4名男生、2名女生站成一排照相.
(1)两女生要在两端,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲要在女生乙的右方(可以不相邻),有多少种不同的站法?
(4)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com