
已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.
(1)求a的值;
(2)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值.]
(1)a=1.(2)
解析试题分析:(1)f(x)的定义域为(-a,+∞).
f ′(x)=1- =
= .
.
由f ′(x)=0,得x=1-a>-a.
当x变化时,f ′(x),f(x)的变化情况如下表:
因此,f(x)在x=1-a处取得最小值,x (-a,1-a) 1-a (1-a,+∞) f ′(x) - 0 + f(x)  ??
??极小值 
故由题意f(1-a)=1-a=0,所以a=1.
(2)当k≤0时,取x=1,有f(1)=1-ln2>0,
故k≤0不合题意.
当k>0时,令g(x)=f(x)-kx2,
即g(x)=x-ln(x+1)-kx2.
g′(x)= -2kx=
-2kx= .
.
令g′ (x)=0,得x1=0,x2= >-1.
>-1.
①当k≥ 时,
时, ≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减.从而对于任意的x∈[0,+∞),总有g(x)≤g(0)=0,即f(x)≤kx2在[0,+∞)上恒成立.
≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减.从而对于任意的x∈[0,+∞),总有g(x)≤g(0)=0,即f(x)≤kx2在[0,+∞)上恒成立.
故k≥ 符合题意.
符合题意.
②当0<k< 时,
时, >0,对于x∈(0,
>0,对于x∈(0, ),g′(x)>0,故g(x)在(0,
),g′(x)>0,故g(x)在(0, )内单调递增.因此当取x0∈(0,
)内单调递增.因此当取x0∈(0, )时,g(x0)>g(0)=0,即f(x0)≤kx
)时,g(x0)>g(0)=0,即f(x0)≤kx 不成立.
不成立.
故0<k< 不合题意.
不合题意.
综上,k的最小值为 .
.
考点:导数的运用
点评:主要是考查了运用导数求解函数单调性,以及函数最值的运用,属于中档题。


科目:高中数学 来源: 题型:解答题
已知函数 ,
,
(1)当 且
且 时,证明:对
时,证明:对 ,
, ;
;
(2)若 ,且
,且 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(3)数列 ,若存在常数
,若存在常数 ,
, ,都有
,都有 ,则称数列
,则称数列 有上界。已知
有上界。已知 ,试判断数列
,试判断数列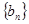 是否有上界.
是否有上界.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(1)求实数 的值;
的值;
(2)求 在区间
在区间 上的最大值;
上的最大值;
(3)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 为
为
直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com