
【题目】已知四棱锥P﹣ABCD,其三视图和直观图如图所示,E为BC中点. (Ⅰ)求此几何体的体积;
(Ⅱ)求证:平面PAE⊥平面PDE.
【答案】解:(Ⅰ)由三视图可知底面ABCD为矩形,AB=2,BC=4, 定点P在面ABCD内的射影为BC的中点E,棱锥的高为2,
∴此几何体的体积 ![]() .
.
证明:(Ⅱ)∵PE⊥平面ABCD,AE平面ABCD,∴PE⊥AE,
取AD中点F,∵AB=CE=BE=2,∴ ![]() ,∴AE⊥ED,
,∴AE⊥ED,
∵ED∩AE=E,∴AE⊥平面PED,∵AE平面PAE,
∴平面PAE⊥平面PDE. 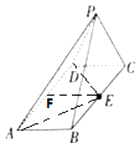
【解析】(Ⅰ)由三视图可知底面ABCD为矩形,AB=2,BC=4,定点P在面ABCD内的射影为BC的中点E,棱锥的高为2,由此能求出此几何体的体积.(Ⅱ)推导出PE⊥AE,AE⊥ED,从而AE⊥平面PED,由此能证明平面PAE⊥平面PDE.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,离心率 ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若经过左焦点F1且倾斜角为 ![]() 的直线l与椭圆交于A、B两点,求|AB|的值.
的直线l与椭圆交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC,若点O是△ABC的内心,则( )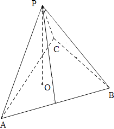
A.PA=PB=PC
B.点P到AB,BC,AC的距离相等
C.PA⊥PB,PB⊥PC,PC⊥PA
D.PA,PB,PC与平面α所成的角相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点. (Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;
(Ⅲ)若AC=4,求几何体C﹣BDF的体积.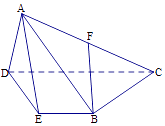
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
(I)求![]() 的值;
的值;
(II)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(III)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分
类舒适型轿车中抽取8辆,经检测它们的得分![]() 的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数
的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数![]() ,设样本平均数为
,设样本平均数为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com