考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)设AC的中点为O,连结EO,OB,由已知条件推导出四边形EFBO是平行四边形,由此能够证明EF∥平面ABC.
(Ⅱ)作BG⊥AC,BH⊥AD,连结GH,则∠BHG是二面角B-AD-C的平面角,由此能求出二面角B-AD-C的大小.
解答:
(Ⅰ)证明:设AC的中点为O,连结EO,OB,
由题意知EO∥BF,且EO=
CC1,BF∥CC
1,且BF=
CC1,
∴EO
CC
1,∴四边形EFBO是平行四边形,
∴EF∥OB,
∵EF不包含于平面ABC,BO?平面ABC,
∴EF∥平面ABC.
(Ⅱ)解:作BG⊥AC,BH⊥AD,连结GH,
∵平面ABC⊥平面AA
1C
1C,∴BG⊥AD,BH∩BG=B,
∴AD⊥平面BHG,∴HG⊥AD,
∴∠BHG是二面角B-AD-C的平面角,
由已知得△ABC为直角三角形,
在Rt△ABC中,
S△ABC=AB•BC=
BG•AC,
∵
AC=2,CC1=2,BC=,
∠ACB=,
∴AB=
,解得BG=
在Rt△ABD中,S
△ABD=
AB•BD=
AD•BH,
∴BH=
,
在Rt△BHG中,sin
∠BHG==
,∴
∠BHG=,
∴二面角B-AD-C的大小为
.
点评:本题考查直线与平面平行的证明,考查二面角的求法,解题时要认真审题,注意空间思维能力的培养.

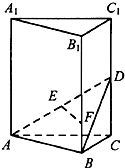 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF

 全能练考卷系列答案
全能练考卷系列答案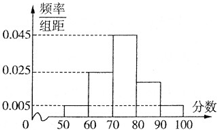 某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有