
已知定义在[-1,1]上的奇函数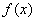 ,当
,当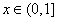 时,
时,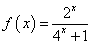 .
.
(1)求函数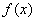 在[-1,1]上的解析式;(2)试用函数单调性定义证明:f(x)在(0,1]上是减函数。
在[-1,1]上的解析式;(2)试用函数单调性定义证明:f(x)在(0,1]上是减函数。
(3)要使方程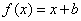 在[-1,1]上恒有实数解,求实数b的取值范围.
在[-1,1]上恒有实数解,求实数b的取值范围.
科目:高中数学 来源: 题型:
设S是至少含有两个元素的集合. 在S上定义了一个二元运算“*”(即对任意的a,b∈S,对于有序元素对(a,b),在S中有唯一确定的元素a*b与之对应). 若对于任意的a,b∈S,有a*( b * a)=b,则对任意的a,b∈S,下列等式中不能成立的是( )
A. ( a * b) * a =a B . [ a*( b * a)] * ( a*b)=a
C. b*( b * b)=b D. ( a*b) * [ b*( a * b)] =b
查看答案和解析>>
科目:高中数学 来源: 题型:
给出定义:若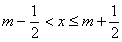 (其中m为整数),则m 叫做离实数x最近的整数,记作
(其中m为整数),则m 叫做离实数x最近的整数,记作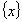 = m. 在此基础上给出下列关于函数
= m. 在此基础上给出下列关于函数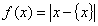 的四个命题: ①函数y=
的四个命题: ①函数y=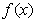 的定义域为R,值域为
的定义域为R,值域为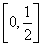 ;
;
②函数y=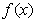 的图像关于直线
的图像关于直线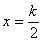 (
(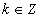 )对称;③函数y=
)对称;③函数y=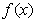 是周期函数,最小正周期为1;
是周期函数,最小正周期为1;
④函数y=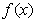 在
在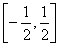 上是增函数。其中正确的命题的序号是 ( )
上是增函数。其中正确的命题的序号是 ( )
A. ① B. ②③ C ①②③ D ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
若集合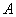 具有以下性质:①
具有以下性质:①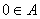 ,
,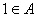 ;②若
;②若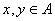 ,则
,则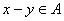 ,且
,且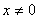 时,
时,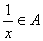 .
.
则称集合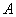 是“好集”.(Ⅰ)分别判断集合
是“好集”.(Ⅰ)分别判断集合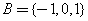 ,有理数集
,有理数集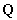 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合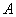 是“好集”,求证:若
是“好集”,求证:若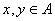 ,则
,则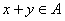 ;(Ⅲ)对任意的一个“好集”
;(Ⅲ)对任意的一个“好集”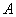 ,
, 分别判断下面命题的真假,并说明理由.命题
分别判断下面命题的真假,并说明理由.命题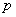 :若
:若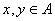 ,则必有
,则必有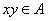 ;命题
;命题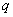 :若
:若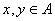 ,且
,且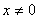 ,则必有
,则必有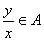 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
由9个正数组成的数阵 每行中的三个数成等差数列,且
每行中的三个数成等差数列,且 ,
, ,
, 成等比数列.给出下列结论: ①第二列中的
成等比数列.给出下列结论: ①第二列中的 必成等比数列; ②第一列中的
必成等比数列; ②第一列中的 不一定成等比数列; ③
不一定成等比数列; ③ ; ④若9个数之和大于81,则
; ④若9个数之和大于81,则 >9.
>9.
其中正确的序号有 .(填写所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com