
分析 根据题意,对$\frac{1}{2x+y}$+$\frac{2}{x+y}$=2变形可得$\frac{1}{2x+y}$+$\frac{1}{x+y}$+$\frac{1}{x+y}$=2,而4x+3y变形可得4x+3y=(2x+y)+(x+y)+(x+y)=$\frac{1}{2}$[(2x+y)+(x+y)+(x+y)]×[($\frac{1}{2x+y}$+$\frac{1}{x+y}$+$\frac{1}{x+y}$)],由柯西不等式分析可得答案.
解答 解:根据题意,若$\frac{1}{2x+y}$+$\frac{2}{x+y}$=2,则有$\frac{1}{2x+y}$+$\frac{1}{x+y}$+$\frac{1}{x+y}$=2,
则4x+3y=(2x+y)+(x+y)+(x+y)
=$\frac{1}{2}$[(2x+y)+(x+y)+(x+y)]×[($\frac{1}{2x+y}$+$\frac{1}{x+y}$+$\frac{1}{x+y}$)]
≥$\frac{1}{2}$[(2x+y)($\frac{1}{2x+y}$)+(x+y)($\frac{1}{x+y}$)+(x+y)($\frac{1}{x+y}$)]2=$\frac{9}{2}$,
即4x+3y的最小值为$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题考查柯西不等式的应用,关键是对$\frac{1}{2x+y}$+$\frac{2}{x+y}$=2和4x+3y的变形.


科目:高中数学 来源: 题型:选择题
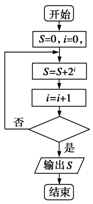
| A. | i=2017? | B. | i≥2017? | C. | i≥2018? | D. | i≤2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
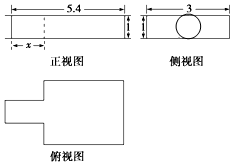 中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )
中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com