
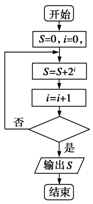
| A. | i=2017? | B. | i≥2017? | C. | i≥2018? | D. | i≤2018? |
分析 按照程序框图的流程写出前几次循环的结果,据要输出的值,判断出直到第几次循环的i值才满足判断框中的条件,从而得到四个选项中的正确答案.
解答 解:经过第一次循环得到结果s=1,i=1,此时不输出,不满足判断框中的条件,
经过第二次循环得到结果s=1+2,i=2,此时不输出,不满足判断框中的条件,
经过第三次循环得到结果s=1+2+22,i=3,此时不输出,不满足判断框中的条件,
…
经过第2018次循环得到结果s=1+2+22+…+22017,i=2018,此时输出,满足判断框中的条件.
即i=1,2,3…2017时不满足判断框中的条件,i=2018时满足判断框中的条件
答案为:i≥2018.
故选C.
点评 本题考查解决程序框图中的循环结构时,常采用写出前几次循环的结果,找规律.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| C. | 横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 纵坐标伸长到原来的$\frac{1}{2}$倍,横坐标不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
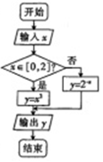 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com