
分析 由题意可知,sinα+cosα=-a,sinα•cosα=2b2,且a2-8b2≥0.由sinα+cosα=-a,结合a为整数可得a=-1或0或1,然后分类求出α,进一步求得b的值验证a2-8b2≥0得答案.
解答 解:∵sinα,cosα是方程x2+ax+2b2=0的两个根,
∴sinα+cosα=-a,sinα•cosα=2b2,且a2-8b2≥0.
由a=-(sinα+cosα)=-$\sqrt{2}sin(α+\frac{π}{4})$$∈[-\sqrt{2},\sqrt{2}]$,且a为整数,
得a=-1或0或1,
若a=-1,则$-\sqrt{2}sin(α+\frac{π}{4})$=-1,sin($α+\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∵0≤α<2π,∴$\frac{π}{4}≤α+\frac{π}{4}<\frac{9π}{4}$,
得$α+\frac{π}{4}=\frac{3π}{4}$,$α=\frac{π}{2}$,
此时b=0,符合a2-8b2≥0;
若a=1,则$-\sqrt{2}sin(α+\frac{π}{4})$=1,sin($α+\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,
∵0≤α<2π,∴$\frac{π}{4}≤α+\frac{π}{4}<\frac{9π}{4}$,
得$α+\frac{π}{4}$=$\frac{5π}{4}$或$α+\frac{π}{4}$=$\frac{7π}{4}$,即α=π或$α=\frac{3π}{2}$,
此时b=0,符合a2-8b2≥0;
若a=0,则$-\sqrt{2}sin(α+\frac{π}{4})$=0,sin($α+\frac{π}{4}$)=0,
∵0≤α<2π,∴$\frac{π}{4}≤α+\frac{π}{4}<\frac{9π}{4}$,
得$α+\frac{π}{4}$=π或$α+\frac{π}{4}$=2π,即α=$\frac{3π}{4}$或$α=\frac{7π}{4}$,
由sinα•cosα=2b2可知b≠0,不满足a2-8b2≥0.
综上,α=$\frac{π}{2}$或α=π或α=$\frac{3π}{2}$.
点评 本题考查三角函数的化简求值,考查了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | x=0,y=2 | B. | x=0,y=-2 | C. | x=2,y=-2 | D. | 不能唯一确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
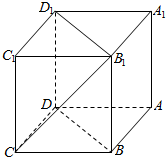 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com