
分析 运用余弦定理,可得c,再由正弦定理,可得A,B.
解答 解:在△ABC中,由a=$\sqrt{3}$+1,b=2,c=$\frac{π}{3}$,
运用余弦定理可得,c2=a2+b2-2abcosC
=($\sqrt{3}$+1)2+22-2($\sqrt{3}$+1)•2•$\frac{1}{2}$=6,
解得c=$\sqrt{6}$,
由正弦定理可得,$\frac{\sqrt{3}+1}{sinA}$=$\frac{2}{sinB}$=$\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$=2$\sqrt{2}$,
即有A=$\frac{5π}{12}$,B=$\frac{π}{4}$.
点评 本题考查解三角形问题,主要考查正弦定理和余弦定理的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥l且l与圆O相交 | B. | m⊥l且l与圆O相切 | C. | m∥l且l与圆O相离 | D. | m⊥l且l与圆O相离 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
从1,2,3,4,5这5个数字中,不放回地任取两数,则两数都是奇数的概率是( )
A.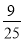 B.
B.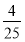 C.
C.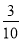 D.
D.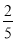
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com