
分析 (1)已知式子平方结合二倍角公式可得;
(2)由题意和完全平方式的特点可得sinα+cosα的值,解方程组可得.
解答 解:(1)∵sinα-cosα=-$\frac{5}{4}$,且-$\frac{π}{4}$<α<0,
∴(sinα-cosα)2=$\frac{25}{16}$,∴1-2sinαcosα=$\frac{25}{16}$,
∴sinαcosα=-$\frac{9}{32}$;
(2)∵(sinα+cosα)2=(sinα-cosα)2+4sinαcosα=$\frac{7}{16}$,
又∵-$\frac{π}{4}$<α<0,∴sinα+cosα>0,∴sinα+cosα=$\frac{\sqrt{7}}{4}$,
联立sinα-cosα=-$\frac{5}{4}$和sinα+cosα=$\frac{\sqrt{7}}{4}$可解得cosα=$\frac{5+\sqrt{7}}{8}$
点评 本题考查三角函数公式和方程的解法,属基础题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | at0 | B. | -at0 | C. | $\frac{1}{2}$at0 | D. | 2at0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程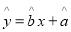 中的
中的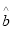 为
为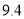 ,据此模型预报广告费用为6万元时销售额为 ( )
,据此模型预报广告费用为6万元时销售额为 ( )
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com