
分析 (1)设等差数列{an}的公差为d,运用调查核实了的通项公式和求和公式,解方程可得d=4,进而得到所求通项公式;
(2)运用数列的求和方法:分组求和和裂项相消求和,结合等比数列的求和公式,化简整理即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,
由题意可得4a1+$\frac{4×3}{2}$d=5(a1+d)+2,
a1=2,解得d=4,
即有an=a1+(n-1)d=4n-2;
(2)由题意可得b1=20+$\frac{16}{4×8}$=1$\frac{1}{2}$;
a2=6,b2=2+$\frac{16}{8×12}$=2$\frac{1}{6}$;
…,
an=4n-2,bn=2n-1+$\frac{16}{4n•(4n+4)}$
=2n-1+$\frac{1}{n}$-$\frac{1}{n+1}$,
即有纵坐标之和Tn=$\frac{1-{2}^{n}}{1-2}$+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=2n-$\frac{1}{n+1}$.
点评 本题考查等差数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和和裂项相消求和,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | at0 | B. | -at0 | C. | $\frac{1}{2}$at0 | D. | 2at0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:填空题
①函数y=cos(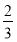 x+
x+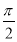 )是奇函数;
)是奇函数;
②存在实数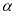 ,使得sin
,使得sin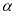 +cos
+cos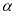 =2;
=2;
③若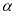 、
、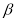 是第一象限角且
是第一象限角且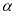 <
<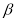 ,则tan
,则tan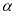 <tan
<tan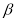 ;
;
④x=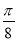 是函数y=sin(2x+
是函数y=sin(2x+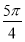 )的一条对称轴方程;
)的一条对称轴方程;
⑤函数y=tan(2x+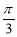 )的图象关于点(
)的图象关于点(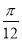 ,0)成中心对称图形.
,0)成中心对称图形.
其中正确命题的序号为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com