
分析 由已知求出A的坐标,代入直线mx+ny+1=0,可得2m+n=1,求出$\frac{1}{m}$+$\frac{1}{n}$取最小值时m,n的值,结合隐含条件求出椭圆的半焦距,代入离心率公式得答案.
解答 解:∵y=ax(a>0且a≠1)的图象恒过定点(0,1),
∴函数y=ax+2-2(a>0且a≠1)的图象恒过定点A(-2,-1),
由点A在直线mx+ny+1=0上,得-2m-n+1=0,
∴2m+n=1,
则$\frac{1}{m}$+$\frac{1}{n}$=($\frac{1}{m}$+$\frac{1}{n}$)(2m+n)=3+$\frac{n}{m}+\frac{2m}{n}$,
∵mn>0,
∴$\frac{1}{m}$+$\frac{1}{n}$=3+$\frac{n}{m}+\frac{2m}{n}$$≥3\sqrt{\frac{n}{m}•\frac{2m}{n}}=3\sqrt{2}$.
当且仅当$\left\{\begin{array}{l}{2m+n=1}\\{\frac{n}{m}=\frac{2m}{n}}\end{array}\right.$,即m=1-$\frac{\sqrt{2}}{2}$,n=$\sqrt{2}-1$时上式等号成立.
∴${a}^{2}={n}^{2}=(\sqrt{2}-1)^{2}=3-2\sqrt{2}$,${c}^{2}={a}^{2}-{b}^{2}=(\sqrt{2}-1)^{2}-(1-\frac{\sqrt{2}}{2})^{2}$=$\frac{3}{2}-\sqrt{2}$,
则${e}^{2}=\frac{{c}^{2}}{{a}^{2}}=\frac{\frac{1}{2}(3-2\sqrt{2})}{3-2\sqrt{2}}=\frac{1}{2}$,
∴e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的简单性质,考查了利用基本不等式求最值,考查椭圆的标准方程,训练了利用椭圆标准方程求椭圆离心率的方法,是中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0,y=2 | B. | x=0,y=-2 | C. | x=2,y=-2 | D. | 不能唯一确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
在区间[-π,π]内随机取两个数分别记为a,b,则使得函数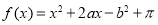 有零点的概率为( )
有零点的概率为( )
A. 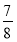 B.
B. 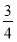 C.
C. 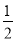 D.
D. 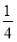
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com