
【题目】已知函数f(x)=x+![]() +2(m为实常数).
+2(m为实常数).
(1)若函数f(x)图象上动点P到定点Q(0,2)的距离的最小值为![]() ,求实数m的值;
,求实数m的值;
(2)若函数y=f(x)在区间[2,+∞)上是增函数,试用函数单调性的定义求实数m的取值范围;
(3)设m<0,若不等式f(x)≤kx在x∈[![]() ,1]时有解,求k的取值范围.
,1]时有解,求k的取值范围.
【答案】(1) ![]() 或
或![]() ;(2)(-∞,4];(3)答案见解析.
;(2)(-∞,4];(3)答案见解析.
【解析】试题分析:
(1)设P(x,y),结合两点之间距离公式有: ![]() ,求解关于实数
,求解关于实数![]() 的方程可得
的方程可得![]() 或
或![]() ;
;
(2)由题意知,任取x1,x2∈[2,+∞),且x1<x2,有f(x2)-f(x1)=(x2-x1)·![]() >0.则m<x1x2.据此可得m的取值范围是(-∞,4].
>0.则m<x1x2.据此可得m的取值范围是(-∞,4].
(3)由f(x)≤kx分离参数可得: ![]() 在
在![]() 上能成立,换元令
上能成立,换元令![]() ,结合二次函数的性质可得:
,结合二次函数的性质可得:
当![]() 时,k∈[4m+5,+∞);
时,k∈[4m+5,+∞);
当![]() 时,k∈[m+3,+∞).
时,k∈[m+3,+∞).
试题解析:
(1)设P(x,y),则y=x+![]() +2,
+2,
PQ2=x2+(y-2)2=x2+(x+![]() )2
)2
=2x2+![]() +2m≥2
+2m≥2![]() |m|+2m=2,
|m|+2m=2,
当m>0时,解得m=![]() -1;
-1;
当m<0时,解得m=-![]() -1.
-1.
所以m=![]() -1或m=-
-1或m=-![]() -1.
-1.
(2)由题意知,任取x1,x2∈[2,+∞),且x1<x2,
则f(x2)-f(x1)=x2+![]() +2-(x1+
+2-(x1+![]() +2)=(x2-x1)·
+2)=(x2-x1)·![]() >0.
>0.
因为x2-x1>0,x1x2>0,
所以x1x2-m>0,即m<x1x2.
由x2>x1≥2,得x1x2>4,所以m≤4.
所以m的取值范围是(-∞,4].
(3)由f(x)≤kx,得x+![]() +2≤kx.
+2≤kx.
因为x∈[![]() ,1],所以k≥
,1],所以k≥![]() +
+![]() +1.
+1.
令t=![]() ,则t∈[1,2],
,则t∈[1,2],
所以k≥mt2+2t+1.
令g(t)=mt2+2t+1,t∈[1,2],
于是,要使原不等式在x∈[![]() ,1]时有解,当且仅当k≥[g(t)]min(t∈[1,2]).
,1]时有解,当且仅当k≥[g(t)]min(t∈[1,2]).
因为m<0,
所以g(t)=m(t+![]() )2+1-
)2+1-![]() 的图象开口向下,
的图象开口向下,
对称轴为直线t=-![]() >0.
>0.
因为t∈[1,2],所以当0<-![]() ≤
≤![]() ,
,
即m≤-![]() 时,g(t)min=g(2)=4m+5;
时,g(t)min=g(2)=4m+5;
当-![]() >
>![]() ,即-
,即-![]() <m<0时,
<m<0时,
g(t)min=g(1)=m+3.
综上,当m≤-![]() 时,k∈[4m+5,+∞);
时,k∈[4m+5,+∞);
当-![]() <m<0时,k∈[m+3,+∞).
<m<0时,k∈[m+3,+∞).


科目:高中数学 来源: 题型:
【题目】函数f(x)=a![]() -2ln x(a∈R).
-2ln x(a∈R).
(Ⅰ)当a=2时,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若a>![]() ,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<
,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856288)
设函数f(x)=aln x-x,g(x)=aex-x,其中a为正实数.
(Ⅰ)若f(x)在(1,+∞)上是单调减函数,且g(x)在(2,+∞)上有最小值,求a的取值范围;
(Ⅱ)若函数f(x)与g(x)都没有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
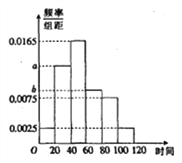
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x+1|﹣|2x﹣3|,g(x)=|x+1|+|x﹣a|.
(l)求f(x)≥1的解集;
(2)若对任意的t∈R,s∈R,都有g(s)≥f(t).求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856295)德国大数学家高斯年少成名,被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》, 在其年幼时,对1+2+3+…+100的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也被称为高斯算法.现有函数f(x)=![]() ,则f(1)+f(2)+…+f(m+2017)等于( )
,则f(1)+f(2)+…+f(m+2017)等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
A. (1,+∞) B. [1,+∞)
C. (2,+∞) D. [2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com