
【题目】函数f(x)=a![]() -2ln x(a∈R).
-2ln x(a∈R).
(Ⅰ)当a=2时,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若a>![]() ,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<
,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<![]() .
.
【答案】(Ⅰ)3x-2y-4ln 2=0(Ⅱ)见解析
【解析】试题分析:(Ⅰ) 求出导数,计算![]() 可得到切线斜率,求出
可得到切线斜率,求出![]() 可得切点坐标,利用点斜式即可求出切线方程;(Ⅱ) 设
可得切点坐标,利用点斜式即可求出切线方程;(Ⅱ) 设![]() 的两根为
的两根为![]() ,所以
,所以![]() ,求出
,求出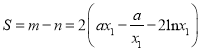 ,将
,将![]() 的值代入
的值代入![]() 的解析式,化简,构造新函数
的解析式,化简,构造新函数![]() ,求导数,利用导数研究函数的单调性,应用单调性求最值,即可证明结论.
,求导数,利用导数研究函数的单调性,应用单调性求最值,即可证明结论.
试题解析:(Ⅰ) f′(x)=a+![]() -
-![]() ,若a=2,则f′(2)=2+
,若a=2,则f′(2)=2+![]() -
-![]() =
=![]() ,f(2)=4-1-2ln 2=3-2ln 2,则曲线f(x)在x=2处的切线方程为y-(3-2ln 2)=
,f(2)=4-1-2ln 2=3-2ln 2,则曲线f(x)在x=2处的切线方程为y-(3-2ln 2)=![]() (x-2),化简得3x-2y-4ln 2=0.
(x-2),化简得3x-2y-4ln 2=0.
(Ⅱ)f′(x)=![]() ,令f′(x)=0,得ax2-2x+a=0,
,令f′(x)=0,得ax2-2x+a=0,
则Δ>0且![]() <a,得
<a,得![]() <a<1,此时设f′(x)=0的两根为x1,x2(x1<x2),
<a<1,此时设f′(x)=0的两根为x1,x2(x1<x2),
所以m=f(x1),n=f(x2).
因为x1x2=1,所以x1<1<x2,由![]() <a<1,
<a<1,
所以S=m-n=ax1-![]() -2ln x1-(ax2-
-2ln x1-(ax2-![]() -2ln x2)
-2ln x2)
=ax1-![]() -2ln x1-(
-2ln x1-(![]() -ax1+2ln x1)
-ax1+2ln x1)
=2(ax1-![]() -2ln x1).
-2ln x1).
由a![]() -2x1+a=0得a=
-2x1+a=0得a=![]() ,
,
代入上式得S=4(![]() -lnx1)
-lnx1)
=4(![]() -
-![]() ln
ln![]() ).
).
令h(x)=ax2-2x+a,则h![]() =
=![]() -
-![]() +a
+a
=a·![]() -
-![]() >
>![]() ·
·![]() -
-![]() =
=![]() -
-![]() =0,
=0,
x=![]()
![]() 是抛物线h(x)的对称轴.
是抛物线h(x)的对称轴.
∴![]() <x1<1.
<x1<1.
令![]() =t,所以
=t,所以![]() <t<1,g(x)=
<t<1,g(x)=![]() -
-![]() ln x,则S=4g(t),
ln x,则S=4g(t),
g'(x)=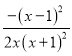 <0,所以g(x)在
<0,所以g(x)在![]() ≤x≤1上为减函数,
≤x≤1上为减函数,
从而g(1)<g(t)<g(![]() ),即0<g(t)<
),即0<g(t)< ![]() ,所以S<
,所以S<![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与极值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方程f(x)+2=![]() 的实数x为( )
的实数x为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(sin x,mcos x),b=(3,-1).
(1)若a∥b,且m=1,求2sin2x-3cos2x的值;
(2)若函数f(x)=a·b的图象关于直线![]() 对称,求函数f(2x)在
对称,求函数f(2x)在![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
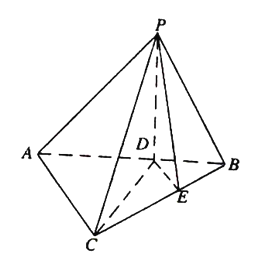
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线M的参数方程为![]() (θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+
(θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+![]() )=
)=![]() t(其中t为常数).
t(其中t为常数).
(Ⅰ)若曲线N与曲线M只有一个公共点,求t的值;
(Ⅱ)当t=-1时,求曲线M上的点与曲线N上的点的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=![]() ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别是a,b,c,且2acosA=bcosC+ccosB.
(Ⅰ)求A的大小;
(Ⅱ)若a=2,求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() +2(m为实常数).
+2(m为实常数).
(1)若函数f(x)图象上动点P到定点Q(0,2)的距离的最小值为![]() ,求实数m的值;
,求实数m的值;
(2)若函数y=f(x)在区间[2,+∞)上是增函数,试用函数单调性的定义求实数m的取值范围;
(3)设m<0,若不等式f(x)≤kx在x∈[![]() ,1]时有解,求k的取值范围.
,1]时有解,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com