分析:方法一(1)先做出辅助线,连接AC1与A1C交于点K,连接DK,根据要证明线与面平行,需要在面上找一条和已知直线平行的直线,找到的直线是DK.
(2)根据二面角D-CA1-C1与二面角D-CA1-A互补,做出辅助线,边做边证作GH⊥CA1,垂足为H,连接DH,则DH⊥CA1,得到∠DHG为二面角D-CA1-A的平面角,解出结果.
方法二(1)以BC的中点O为原点建系,根据要用的点的坐标,写出对应的向量的坐标,设出一个平面的法向量,求出法向量.根据法向量与已知直线的方向向量的数量积等于0,得到结论.
(2)以BC的中点O为原点建系,根据要用的点的坐标,写出对应的向量的坐标,设出一个平面的法向量,根据法向量与平面上的两个向量垂直且数量积等于0,得到一个法向量,另一个平面的法向量可以直接写出,根据两个平面的法向量所成的角的余弦值求出二面角的余弦值.
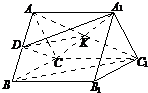
解答:(方法一)(1)证明:如图一,连接AC
1与A
1C交于点K,连接DK.
在△ABC
1中,D、K为中点,∴DK∥BC
1.
又DK?平面DCA
1,BC
1?平面DCA
1,
∴BC
1∥平面DCA
1(2)解:二面角D-CA
1-C
1与二面角D-CA
1-A互补.
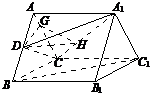
如图二,作DG⊥AC,垂足为G,
又平面ABC⊥平面ACC
1A
1,∴DG⊥平面ACC
1A
1.
作GH⊥CA
1,垂足为H,连接DH,则DH⊥CA
1,
∴∠DHG为二面角D-CA
1-A的平面角
设AB=BC=CA=AA
1=2,
在等边△ABC中,D为中点,∴
AG=AC,在正方形ACC
1A
1中,
GH=AC1,
∴
DG=,
GH=×2=,∴
DH=.
∴
cos∠DHG===.
∴所求二面角的余弦值为
-.
图一 图二 图三
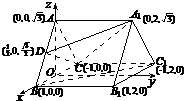
(方法二)(1)证明:如图三以BC的中点O为原点建系,设AB=BC=CA=AA
1=2.
设
=(x,y,z)是平面DCA
1的一个法向量,
则
.又
=(,0,),
=(1,2,),
∴
.令
x=1,z=-,y=1,∴
=(1,1,-)∵
=(-2,2,0),∴
•=-2+2+0=0.
又BC
1?平面DCA
1,∴BC
1∥平面DCA
1.
(2)解:设
=(x1,y1,z1)是平面CA
1C
1的一个法向量,
则
.又
=(0,2,0),
=(1,2,),
∴
.令
z1=1,x1=-,∴
=(-,0,1).
∴
cos< ,>==-.
∴所求二面角的余弦值为
-.
点评:本小题主要考查立体几何的相关知识,具体涉及到线面的平行关系、二面角的求法及空间向量在立体几何中的应用,本题可以利用空间向量来解题从而降低了题目的难度.

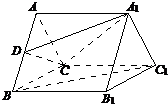 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=CA=AA1,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=CA=AA1,D为AB的中点.




 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.