解:(1)
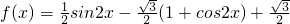
=
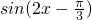
. 又x∈[0,π],故
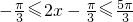
.
在同一坐标系中,作出函数y=sinu

的图象和直线y=m的图象.如图易知,
两图象有两个公共点时,m的取值范围为
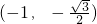
∪

.
又由于
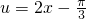
是单调函数,x与u是一一对应,故上述范围即为所求.

(2)由图知,直线y=

分函数y=sinu

图象成上下两部分,上、下两部分的图象分别关于直线u=

与u=

对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分

与

.
当

时,函数y=sinu

的图象为直线y=

的上面部分,它关于直线u=

对称,
于是sinu=m的两根之和为:u
1+u
2=2×

=π,从而函数g(x)的两零点之和为:
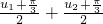
=

;
当

时,函数y=sinu

的图象为直线y=

的下面部分,它关于直线u=

对称,
于是sinu=m的两根之和为:u
1+u
2=2×

=3π,从而函数g(x)的两零点之和为:
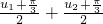
=

.
综上所述,函数两零点之和为

或

.
分析:(1)化简 f(x)=
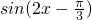
,在同一坐标系中,作出函数y=sinu

的图象和直线y=m的图象,
如图易知,满足条件的 m的取值范围为
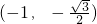
∪

.
(2)当

时,函数y=sinu

的图象关于直线u=

对称,g(x)的两零点之和为:
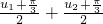
=

;当

时,函数y=sinu

的图象关于直线u=

对称,
函数g(x)的两零点之和为:
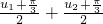
=

.
点评:本题考查两角和差的正弦公式,正弦函数的单调性,对称性,体现了数形结合的数学思想,在同一坐标系中,作出函数y=sinu

的图象和直线y=m的图象,是解题的关键.

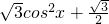 ,x∈[0,π],函数g(x)=f(x)-m有两个不相等的零点.
,x∈[0,π],函数g(x)=f(x)-m有两个不相等的零点.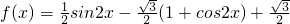 =
=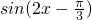 . 又x∈[0,π],故
. 又x∈[0,π],故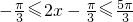 .
. 的图象和直线y=m的图象.如图易知,
的图象和直线y=m的图象.如图易知,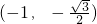 ∪
∪ .
.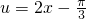 是单调函数,x与u是一一对应,故上述范围即为所求.
是单调函数,x与u是一一对应,故上述范围即为所求.
 分函数y=sinu
分函数y=sinu 图象成上下两部分,上、下两部分的图象分别关于直线u=
图象成上下两部分,上、下两部分的图象分别关于直线u=
 对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分
对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分 与
与 .
. 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的上面部分,它关于直线u=
的上面部分,它关于直线u= 对称,
对称, =π,从而函数g(x)的两零点之和为:
=π,从而函数g(x)的两零点之和为: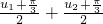 =
= ;
; 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的下面部分,它关于直线u=
的下面部分,它关于直线u= 对称,
对称, =3π,从而函数g(x)的两零点之和为:
=3π,从而函数g(x)的两零点之和为: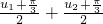 =
= .
. 或
或 .
.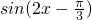 ,在同一坐标系中,作出函数y=sinu
,在同一坐标系中,作出函数y=sinu 的图象和直线y=m的图象,
的图象和直线y=m的图象,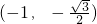 ∪
∪ .
. 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,g(x)的两零点之和为:
对称,g(x)的两零点之和为: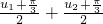 =
= ;当
;当 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,
对称,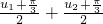 =
= .
. 的图象和直线y=m的图象,是解题的关键.
的图象和直线y=m的图象,是解题的关键. 

 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案