Question

【题目】已知函数．

（1）当时，求函数的单调递减区间；

（2）当时，设函数．若函数在区间上有两个零点，求实数的取值范围．

Answer 1

【答案】（1）当时，的单调递减区间为，当时，的单调递减区间为，当时，的单调递减区间为；（2）.

【解析】

试题分析：（1）讨论当时，当时，当时三种情况，得增区间，得减区间；（2）在上有零点，即关于的方程在上有两个不相等的实数根，可证当时单调递减，当时单调递增，故.

试题解析：（1）的定义域为，．

①当时，，由，

得或．

∴当时，单调递减．

∴的单调递减区间为．

②当时，恒有，

∴的单调递减区间为．

③当时，，由，得或．

∴当时，单调递减．

∴的单调递减区间为．

综上，当时，的单调递减区间为；

当时，的单调递减区间为；

当时，的单调递减区间为．

（2）在上有零点，

即关于的方程在上有两个不相等的实数根．

令函数．

则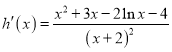，令函数．

则在上有．

故在上单调递增．

∵．

∴当时，有即．

∴单调递减；

当时，有，即，∴单调递增．

∵，

，

∴的取值范围为．