
分析 (I)利用递推关系与等比数列的通项公式即可得出.
(II)利用“裂项求和”方法即可得出;
(III)利用二次函数与数列的单调性即可得出.
解答 (Ⅰ)解:n≥2时,∵Sn+an+n=0,
∴Sn-1+an-1+n-1=0,两式相减可得,2an=an-1-1,
∴2(an+1)=an-1+1,
∵S1+a1+1=2a1+1=0,∴${a_1}=-\frac{1}{2}$,∴${a_1}+1=\frac{1}{2}$,
∴{an+1}是以$\frac{1}{2}$为首项,$\frac{1}{2}$为公比的等比数列,
∴${a_n}+1={(\frac{1}{2})^n}$,∴${a_n}={(\frac{1}{2})^n}-1(n∈{N^*})$.
(II)证明:由(Ⅰ)知,$\frac{1}{{{2^n}{a_n}{a_{n+1}}}}=\frac{1}{{{2^n}(\frac{1}{2^n}-1)(\frac{1}{{{2^{n+1}}}}-1)}}=2(\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}})$,
∴$\frac{1}{{2{a_1}{a_2}}}+\frac{1}{{{2^2}{a_2}{a_3}}}+…+\frac{1}{{{2^n}{a_n}{a_{n+1}}}}=-2(\frac{1}{{{2^1}-1}}-\frac{1}{{{2^2}-1}}+\frac{1}{{{2^2}-1}}$$-\frac{1}{{{2^3}-1}}+…+\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}})=2(\frac{1}{{{2^1}-1}}-\frac{1}{{{2^{n+1}}-1}})=2(1-\frac{1}{{{2^{n+1}}-1}})<2$,
即$\frac{1}{{2{a_1}{a_2}}}+\frac{1}{{{2^2}{a_2}{a_3}}}+…+\frac{1}{{{2^n}{a_n}{a_{n+1}}}}<2$.
( III)∵${x^2}+\frac{1}{2}x-1≥{a_n}$,∴${x^2}+\frac{1}{2}x≥{a_n}+1=\frac{1}{2^n}$,即${x^2}+\frac{1}{2}x≥{(\frac{1}{2^n})_{max}}=\frac{1}{2}$ 在(-∞,λ]上恒成立,
由${x^2}+\frac{1}{2}x≥\frac{1}{2}$,即2x2+x-1≥0,x≤-1或$x≥\frac{1}{2}$,
∴λ≤-1,即所求λ的取值范围(-∞,-1].
点评 本题考查了递推关系、等比数列的通项公式、“裂项求和”方法、二次函数与数列的单调性,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-$\frac{1}{2}$) | B. | (-1,-$\frac{1}{2}$) | C. | (1,-1) | D. | (-1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
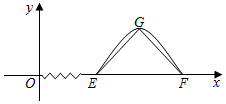 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com