
分析 确定以PQ为直径的圆经过F1,可得|PQ|=2c=10,设F2为双曲线C:$\frac{{x}^{2}}{14}$-$\frac{{y}^{2}}{11}$=1的右焦点,则根据双曲线的对称性,可得|PF1|=|QF2|,利用双曲线的定义,结合勾股定理,即可得出结论.
解答 解:由题意,直线l过原点且与双曲线C相交于P,Q两点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
∴PF1⊥PF2,
∴|OP|=c,
∴|PQ|=2c=10,
设F2为双曲线C:$\frac{{x}^{2}}{14}$-$\frac{{y}^{2}}{11}$=1的右焦点,则根据双曲线的对称性,可得|PF1|=|QF2|,
∴|QF1|-|PF1|=2$\sqrt{14}$,
∵|QF1|2+|PF1|2=100,
∴2|QF1||PF1|=44,
∴(|QF1|+|PF1|)2=144,
∴|QF1|+|PF1|=12,
∴△PF1Q的周长等于22,
故答案为:22.
点评 本题考查双曲线的性质,考查向量知识的运用,考查学生分析解决问题的能力,正确运用双曲线的定义是关键.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
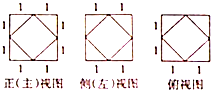
| A. | $\frac{26}{3}$ | B. | $\frac{25}{3}$ | C. | $\frac{22}{3}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
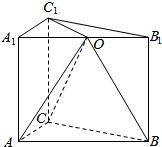 如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com