
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 由二维到三维的类比推理要注意点的性质往往推广为线的性质,线的性质往往推广为面的性质.
解答 解:将其类比到空间则有:四面体中,
①在四面体ABCD中,设点A在底面上的射影为O,则三个侧面的面积都大于在底面上的投影的面积,故三个侧面的面积之和一定大于底面的面积,所以任意三个面的面积之和大于第四个面的面积,正确;
②由平面几何中线的性质,类比推理空间几何中面的性质,可得过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的$\frac{1}{4}$,正确;
③利用分割法,若内切球半径为R,表面积为s,则体积V=$\frac{1}{3}$sR,正确;
④四面体都有外接球,正确.
故选:D.
点评 本题考查类比推理,体现了数形结合的数学思想,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 推理完全正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 推理形式不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7.5 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
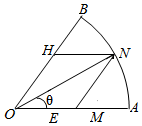 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,+∞) | C. | (0,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com