�ȼ���Ʒһ�ȶ��ȼ�5����Ԫ��2.5����Ԫ����2.5����Ԫ��1.5����Ԫ��������Ŀ��Ʒ���ˣ������ʽ���Ԫ����88��210���������Ʒ��һ����ڶ������0.80.85��0.750.8����ij���������ס������ֲ�Ʒ��ÿ�ֲ�Ʒ���Ǿ�����һ�͵ڶ�����ӹ����ɣ���������ļӹ�����������ÿ������ļӹ��������A��B�����ȼ�����ÿ�ֲ�Ʒ����������ļӹ������ΪA��ʱ����ƷΪһ��Ʒ�������Ϊ����Ʒ��
��1����֪�ס������ֲ�Ʒÿһ������ļӹ����ΪA���ĸ������һ��ʾ���ֱ����������ļס��Ҳ�ƷΪһ��Ʒ�ĸ���P
����P
����
��2����֪һ����Ʒ�������������ʾ���æΡ��Ƿֱ��ʾһ���ס��Ҳ�Ʒ�������ڣ�1���������£���Ρ��ǵķֲ��м�E�Ρ�E�ǣ�
��3����֪����һ����Ʒ���õĹ��������ʽ���������ʾ���ù����й���40���������ʣ���60��Ԫ����x��y�ֱ��ʾ�����ס��Ҳ�Ʒ���������ڣ�II���������£�x��yΪ��ֵʱ��Z=xE��+yE��������ֵ�Ƕ��٣������ʱ�����ͼʾ��






 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
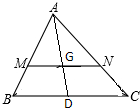 ��ͼ����ABC�У�DΪBC���е㣬GΪAD���е㣬����G����һֱ��MN���ֱ�AB��AC��M��N���㣬��
��ͼ����ABC�У�DΪBC���е㣬GΪAD���е㣬����G����һֱ��MN���ֱ�AB��AC��M��N���㣬��