
| x2 |
| 16 |
| y2 |
| 7 |
| x2 |
| 16 |
| y2 |
| 7 |
| (2+3)2+(1-0)2 |
| 26 |
| 26 |
| 26 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示的是某单位的男职工进行健康体检时的体重情况的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24,那么该单位共有男职工的人数为( )
如图所示的是某单位的男职工进行健康体检时的体重情况的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24,那么该单位共有男职工的人数为( )| A、150 | B、120 |
| C、48 | D、96 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| k |
| 4-x2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
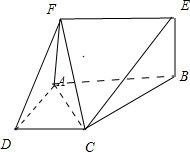 已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4
已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com