
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E是
,E是![]() 的中点.现将
的中点.现将![]() 沿
沿![]() 翻折,使点A移动至平面
翻折,使点A移动至平面![]() 外的点P.
外的点P.
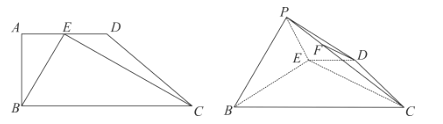
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)法一:在线段![]() 上取靠近点P的四等分点G,连接
上取靠近点P的四等分点G,连接![]() ,
,![]() ,证出四边形
,证出四边形![]() 为平行四边形,从而可得
为平行四边形,从而可得![]() ,再利用线面平行的判定定理即可证出. 法二:在线段
,再利用线面平行的判定定理即可证出. 法二:在线段![]() 上取靠近点B的四等分点H,连接
上取靠近点B的四等分点H,连接![]() ,
,![]() ,证出
,证出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,利用面面平行的判定定理可得平面
,利用面面平行的判定定理可得平面![]() 平面
平面![]() ,再利用面面平行的性质定理即可证出.
,再利用面面平行的性质定理即可证出.
(2)以E为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过点E垂直平面
轴,过点E垂直平面![]() 的垂线为
的垂线为![]() 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的一个法向量,取平面
的一个法向量,取平面![]() 的一个法向量为
的一个法向量为![]() ,利用空间向量的数量积即可求解.
,利用空间向量的数量积即可求解.
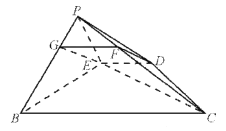
(1)法一:依题意得![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
如图,在线段![]() 上取靠近点P的四等分点G,连接
上取靠近点P的四等分点G,连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() ,
,![]()
所以四边形![]() 为平行四边形,可得
为平行四边形,可得![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
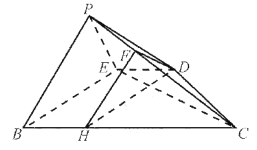
法二:如图,在线段![]() 上取靠近点B的四等分点H,连接
上取靠近点B的四等分点H,连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
依题意得![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
而![]() ,所以
,所以![]() ,
,![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(2)由![]() ,得
,得![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
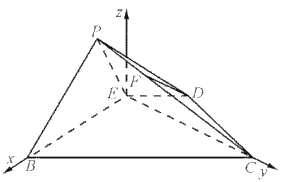
以E为原点,建立如图所示空间直角坐标系![]() ,
,
则![]() ,
,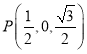 ,
,![]() ,
,![]() ,
,
由![]() ,得
,得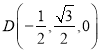
则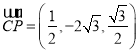 ,
,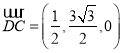 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则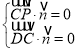 ,即
,即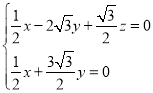 ,
,
故可取![]()
又![]() 平面
平面![]() ,可取平面
,可取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则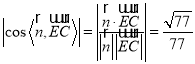 .
.
所以,平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设集合S,T,S![]() N*,T
N*,T![]() N*,S,T中至少有两个元素,且S,T满足:
N*,S,T中至少有两个元素,且S,T满足:
①对于任意x,y![]() S,若x≠y,都有xy
S,若x≠y,都有xy![]() T
T
②对于任意x,y![]() T,若x<y,则
T,若x<y,则![]()
![]() S;
S;
下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为加强对销售员的考核与管理,从销售部门随机抽取了2019年度某一销售小组的月均销售额,该小组各组员2019年度的月均销售额(单位:万元)分别为:3.35,3.35,3.38,3.41,3.43,3.44,3.46,3.48,3.51,3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
(Ⅰ)根据公司人力资源部门的要求,若月均销售额超过3.52万元的组员不低于全组人数的![]() ,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
(Ⅱ)在该销售小组中,已知月均销售额最高的5名销售员中有1名的月均销售额造假.为找出月均销售额造假的组员,现决定请专业机构对这5名销售员的月均销售额逐一进行审核,直到能确定出造假组员为止.设审核次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某口罩厂一年中各月份的收入、支出情况如图所示(单位:万元,下列说法中错误的是(注:月结余=月收入一月支出)( )
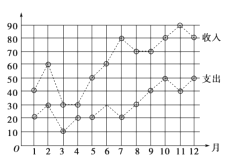
A.上半年的平均月收入为45万元B.月收入的方差大于月支出的方差
C.月收入的中位数为70D.月结余的众数为30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a=-2时,求函数f(x)的极值;
(2)若ln[e(x+1)]≥2- f(-x)对任意的x∈[0,+∞)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线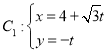 (t为参数),曲线
(t为参数),曲线![]() ,(
,(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 分别交
分别交![]() ,
,![]() 于A,B两点,求
于A,B两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com