
分析 (Ⅰ)求出f′(x)=ex-1(x+1)(x-n),分n>-1,n<-1和n=-1分析原函数的单调区间;
(Ⅱ)当f(x)在R上单调递增时,n=-1,此时f(x)=(x2+1)ex-1,则g(x)=$\frac{f(x)}{{x}^{2}+1}$=$\frac{({x}^{2}+1){e}^{x-1}}{{x}^{2}+1}={e}^{x-1}$.不妨设x1<x2,则x2-x1>0.把要证不等式$\frac{g({x}_{2})+g({x}_{1})}{2}$>$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$转化为证x2-x1>2$\frac{{e}^{{x}_{2}-{x}_{1}}-1}{{e}^{{x}_{2}-{x}_{1}}+1}$,令x2-x1=t,则t>2$\frac{{e}^{t}-1}{{e}^{t}+1}$,即et(t-2)+t+2>0.构造函数h(t)=et(t-2)+t+2,利用两次求导可得h(t)为(0,+∞)上的增函数,则h(t)>h(0)=0.即$\frac{g({x}_{2})+g({x}_{1})}{2}$>$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$.
解答 (Ⅰ)解:f′(x)=ex-1(x+1)(x-n),
若n>-1,则当x∈(-∞,-1)∪(n,+∞)时,f′(x)>0,当x∈(-1,n)时,f′(x)<0,
∴f(x)的增区间为(-∞,-1),(n,+∞),减区间为(-1,n);
若n<-1,则当x∈(-∞,n)∪(-1,+∞)时,f′(x)>0,当x∈(n,-1)时,f′(x)<0,
∴f(x)的增区间为(-∞,n),(-1,+∞),减区间为(n,-1);
若n=-1,则f′(x)=ex-1(x+1)2≥0,函数f(x)在R上为增函数.
(Ⅱ)证明:当f(x)在R上单调递增时,n=-1,此时f(x)=(x2+1)ex-1,
g(x)=$\frac{f(x)}{{x}^{2}+1}$=$\frac{({x}^{2}+1){e}^{x-1}}{{x}^{2}+1}={e}^{x-1}$.
不妨设x1<x2,则x2-x1>0.
要证不等式$\frac{g({x}_{2})+g({x}_{1})}{2}$>$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$,即证$\frac{{e}^{{x}_{2}-1}+{e}^{{x}_{1}-1}}{2}$>$\frac{{e}^{{x}_{2}-1}-{e}^{{x}_{1}-1}}{{x}_{2}-{x}_{1}}$,
即x2-x1>2$\frac{{e}^{{x}_{2}}-{e}^{{x}_{1}}}{{e}^{{x}_{2}}+{e}^{{x}_{1}}}$,也就是x2-x1>2$\frac{{e}^{{x}_{2}-{x}_{1}}-1}{{e}^{{x}_{2}-{x}_{1}}+1}$,
令x2-x1=t,则t>2$\frac{{e}^{t}-1}{{e}^{t}+1}$,即et(t-2)+t+2>0.
令h(t)=et(t-2)+t+2,则h′(t)=et(t-1)+1.
而h″(t)=tet>0,∴h′(t)>h′(0)=0.
则h(t)为(0,+∞)上的增函数,
∴h(t)>h(0)=0.
∴$\frac{g({x}_{2})+g({x}_{1})}{2}$>$\frac{g({x}_{2})-g({x}_{1})}{{x}_{2}-{x}_{1}}$.
点评 不妥考查利用导数研究函数的单调性,考查数学转化、分类讨论等数学思想方法,属难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({2^x})<f(\frac{lna}{a})<f[{(\frac{lna}{a})^2}]$ | B. | $f(\frac{lna}{a})<f[{(\frac{lna}{a})^2}]<f({2^x})$ | ||
| C. | $f(\frac{lna}{a})<f({2^x})<f[{(\frac{lna}{a})^2}]$ | D. | $f({2^x})<f[{(\frac{lna}{a})^2}]<f(\frac{lna}{a})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | n | C. | 2n | D. | 4n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
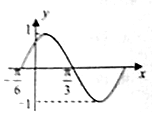 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )
函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为假 | B. | ¬q为真 | C. | p∨q为真 | D. | p∧q为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{8}{3}$ | B. | $-\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com