
分析 (1)欲求a的值的大小,根据所给的切线方程,只须求出切线斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率进而得切线方程,最后与所给的方程比较即得a的值.
(2)欲求函数f(x)单调区间,先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0即得.
解答 解:(1)f'(x)=ex[x2-(1+a)x+1]+ex(2x-1-a)=ex[x2+(1-a)x-a]=ex(x-a)(x+1),
由曲线y=f(x)在点P(0,f(0))处的切线与直线平行y=x+4,
得f'(0)=1,即e0(0-a)(0+1)=1,解得,a=-1.
(2)∵ex>0,令f'(x)=0,得x=a或x=-1.∴①若a=-1,f'(x)≥0,f(x)是增函数,增区间为(-∞,+∞).(7分)
②若a<-1,当x<a或x>-1时,f'(x)>0,f(x)是增函数,增区间为(-∞,a),(-1,+∞).
当a<x<-1时,f'(x)<0,f(x)是减函数,减区间为(a,-1).(10分)
③若a>-1,当x<-1或x>a时,f'(x)>0,f(x)是增函数,增区间为(-∞,-1),(a,+∞).
当-1<x<a时,f'(x)<0,f(x)是减函数,减区间为(-1,a).(13分)
点评 本小题主要考查利用导数研究函数的单调性、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
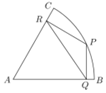 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6,+∞) | B. | (-∞,-6]∪[6,+∞) | C. | (6,+∞) | D. | (-6,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
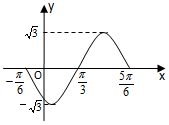 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com