
分析 由已知函数可求得,$f(x)+f(-\frac{1}{x})$=-2,代入即可求解.
解答 解:∵f(x)=$\frac{2{x}^{2}}{1-x^2}$,
∴$f(x)+f(-\frac{1}{x})$=$\frac{2{x}^{2}}{1-{x}^{2}}+\frac{2(-\frac{1}{x})^{2}}{1-(-\frac{1}{x})^{2}}$=$\frac{2{x}^{2}}{1-{x}^{2}}+\frac{2}{{x}^{2}-1}$=-2,
则f(-10)+f(-9)+f(-8)+…+f(-2)+f($\frac{1}{2}$)+f($\frac{1}{3}$)+…+f($\frac{1}{10}$)
=[f(-2)+f($\frac{1}{2}$)]+[f(-3)+f($\frac{1}{3}$)]+…+[f(-10)+f($\frac{1}{10}$)]
=-2×9=-18.
故答案为:-18
点评 本题主要考查了函数值的求解,解题的关键是发现函数值的规律:$f(x)+f(-\frac{1}{x})$=-2


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥1或m≤-1 | B. | -$\sqrt{3}$≤m≤-1或1≤≤m≤$\sqrt{3}$ | C. | -1≤m≤1 | D. | -$\sqrt{3}$<m≤-1或1≤m<$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
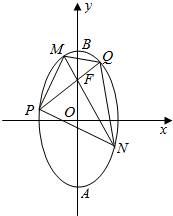 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com