
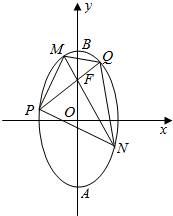
 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.分析 (1)由题意设出椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1(a>b>0)$,并求得c=1,结合$\overrightarrow{AF}•\overrightarrow{FB}=1$,可得a2-c2=1,则a2,b2可求,椭圆方程可求;
(2)由对角线PQ,MN互相垂直,可得直线PQ,MN中至少有一条斜率存在,
不妨设PQ的斜率为k,可得PQ的方程为y=kx+1,联立直线方程和椭圆方程,利用弦长公式求得|PQ|,同理求得|MN|,代入四边形的面积公式后换元,由函数的单调性求得四边形MPNQ面积的最大值和最小值.
解答 解:(1)设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1(a>b>0)$,由题意可知c=1,
∵$\overrightarrow{AF}•\overrightarrow{FB}=1$,∴(a+c)(a-c)=1,即a2-c2=1,
∴a2=2,b2=a2-c2=1,
故椭圆的方程为${x}^{2}+\frac{{y}^{2}}{2}=1$;
(2)∵对角线PQ,MN互相垂直,∴直线PQ,MN中至少有一条斜率存在,
不妨设PQ的斜率为k,又PQ过点F(0,1),故PQ的方程为y=kx+1,将此式代入椭圆方程可得,(2+k2)x2+2kx-1=0,
设P(x1,y1),Q(x2,y2),则${x}_{1}+{x}_{2}=-\frac{2k}{2+{k}^{2}},{x}_{1}{x}_{2}=-\frac{1}{2+{k}^{2}}$,
从而|PQ|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}•\sqrt{(-\frac{2k}{2+{k}^{2}})^{2}+\frac{4}{2+{k}^{2}}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{2+{k}^{2}}$,
当k≠0时,MN的斜率为$-\frac{1}{k}$,同上可得$|MN|=\frac{2\sqrt{2}[1+(-\frac{1}{k})^{2}]}{2+(-\frac{1}{k})^{2}}=\frac{2\sqrt{2}(1+\frac{1}{{k}^{2}})}{2+\frac{1}{{k}^{2}}}$,
故四边形MPNQ的面积$S=\frac{1}{2}|PQ|•|MN|=\frac{4(1+{k}^{2})(1+\frac{1}{{k}^{2}})}{(2+{k}^{2})(2+\frac{1}{{k}^{2}})}$=$\frac{4(2+{k}^{2}+\frac{1}{{k}^{2}})}{5+2{k}^{2}+\frac{2}{{k}^{2}}}$,
令$u={k}^{2}+\frac{1}{{k}^{2}}≥2$,当且仅当k=±1时,u=2,
此时$S=\frac{4(2+u)}{5+2u}=2(1-\frac{1}{5+2u})$,显然S是以u为自变量的增函数,
∴$\frac{16}{9}≤S<2$;
当k=0时,|MN|=$2\sqrt{2}$,|PQ|=$\sqrt{2}$,此时$S=\frac{1}{2}×2\sqrt{2}×\sqrt{2}=2$,
综上所述,四边形MPNQ面积的最大值为2,最小值为$\frac{16}{9}$.
点评 本题考查椭圆方程的求法,考查直线和椭圆位置关系的应用,训练了函数值域的求法,灵活变形及适当的换元是解答该题的关键,是中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{2}$y=0 | D. | 2x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
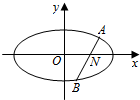 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 18 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com